本發明屬于通信領域，涉及無線通信中的物理層安全技術領域，具體涉及兩種基于中斷概率約束的MISO竊聽信道魯棒波束成形方法。

背景技術：

近年來，無線通信技術的持續發展使得人們可以隨時隨地接入通信網絡。然而，無線傳播的廣播特性意味著傳輸范圍內的所有節點都能夠接收到信源發送的信號，合法用戶的信息容易被竊聽用戶獲取。因此，保證無線通信的安全傳輸變得尤為重要[1]。相對于傳統的加密方法，物理層安全旨在利用無線通信的物理層特性，如噪聲、衰落等，以信息論中的理論為基礎保證無線通信的安全性。

1975年Wyner首次定義了含噪的竊聽信道模型，并且證明當竊聽信道的信噪比比主信道低時可以實現完全的保密通信，并將不依靠密鑰仍可以保證主信道信息可靠傳輸的速率定義為保密速率[2]。進入20世紀末，MIMO技術的出現極大推動了無線通信技術的發展，多天線技術為無線通信物理層安全帶來了新的機遇與挑戰，近年來，已有大量文獻研究利用多天線技術提高物理層安全的保密速率[3]-[5]。對于多天線系統來講，以保密速率為目標，對發射信號進行空間分布設計是研究熱點。在此類設計中，波束成形技術是其中的重要設計參數。波束成形技術通過將信息流引向合法用戶來提高通信效率。

然而，波束成形的物理層安全傳輸性能很大程度上依賴于發射機獲取的信道狀態信息。在MISO竊聽信道模型中，現有的研究大多基于發射機可以獲取理想的主信道和竊聽信道狀態信息的假設[6]-[7]。但是，在實際應用中，由于信道的動態變化和信道估計誤差、量化誤差、反饋時延等因素的影響，發射端獲取的信道狀態信息均有可能出現誤差[8]。很多研究者也考慮了發射端獲取的合法用戶的信道狀態信息存在誤差的情況。然而，現有的物理層安全魯棒波束成形技術的研究多是從最差情況的角度出發來提高保密速率[9]-[10]。由于極端情況發生概率較低，這種設計方式顯得較為保守，不能很好提高系統性能。因此針對非理想信道狀態信息設計基于中斷概率的魯棒性物理層安全傳輸算法是很有必要的。

馬等人[11]考慮了MISO竊聽信道下多種非理想的合法用戶和竊聽用戶信道模型。然而，關于發射端獲取的信道狀態信息，他們沒有考慮如下這種情況：1)合法用戶的信道狀態信息存在誤差；2)竊聽信道僅僅是統計信道狀態信息。我們知道竊聽用戶大多不是發送者和合法用戶所在通信系統中的一部分，因此發送端很難獲得精確的竊聽信道狀態信息。

另外，在物理層安全傳輸設計中，有人工噪聲輔助可以更加有效地降低竊聽用戶的信噪比，達到干擾竊聽用戶，提高保密速率的目的[12]-[13]。唐等人在合法用戶和竊聽用戶信道狀態信息均存在誤差的情況下，通過有人工噪聲輔助以最大化保密速率[14]。但是，他們只是對有用信號和人工噪聲的功率分配進行了優化設計，沒有考慮波束成形設計。

參考文獻：

[1]Chen X,Li F,Xue Z,et al.Research on the Security of MISO Wireless Channel with Artificial Noise[C]//International Conference on Computational&Information Sciences.2013:1533-1536.

[2]Wyner AD.The wire-tap channel[J].Bell System Technical Journal,1975,54(8):1355-1387.

[3]Zhang,Haiyang,Wang,et al.The achievable secrecy rate of MISO wiretap channels[C]//Wireless Communications and Signal Processing(WCSP),2011International Conference on.IEEE,2011:1-4.

[4]Xiong Q,Gong Y,Liang Y C.Achieving secrecy capacity of MISO fading wiretap channels with artificial noise[J].2013:2452-2456.

[5]Li,Q,Ma,et al.Optimal and Robust Transmit Designs for MISO Channel Secrecy by Semidefinite Programming[J].IEEE Transactions on Signal Processing,2011,59(8):3799-3812.

[6]Negi R,Goel S.Secret communication using artificial noise[J].2005,3:1906-1910.

[7]Xiong Q,Gong Y,Liang Y C.Achieving secrecy capacity of MISO fading wiretap channels with artificial noise[J].2013:2452-2456.

[8]Pascual-Iserte A,Palomar D P,Perez-Neira AI,et al.Arobust maximin approach for MIMO communications with imperfect channel state information based on convex optimization[J].Signal Processing IEEE Transactions on,2006,54(1):346-360.

[9]Shi W,Ritcey J.Robust beamforming for MISO wiretap channel by optimizing the worst-case secrecy capacity[C]//2010:300-304.

[10]Li J,Petropulu AP.Explicit Solution of Worst-Case Secrecy Rate for MISO Wiretap Channels With Spherical Uncertainty[J].IEEE Transactions on Signal Processing,2011,60(60):3892-3895.

[11]Ma S,Hong M,Song E,et al.Outage Constrained Robust Secure Transmission for MISO Wiretap Channels[J].IEEE Transactions on Wireless Communications,2013,13(10):5558-5570.

[12]Liao,Wei Cheng,et al."QoS-Based Transmit Beamforming in the Presence of Eavesdroppers:An Optimized Artificial-Noise-Aided Approach."IEEE Transactions on Signal Processing 59.3(2011):1202-1216.

[13]Li Q,Ma W K.Spatially Selective Artificial-Noise Aided Transmit Optimization for MISO Multi-Eves Secrecy Rate Maximization[J].IEEE Transactions on Signal Processing,2013,61(10):2704-2717.

[14]Tang Y,Xiong J,Ma D,et al.Robust Artificial Noise Aided Transmit Design for MISO Wiretap Channels with Channel Uncertainty[J].IEEE Communications Letters,2013,17(11):2096-2099.

技術實現要素：

本發明的目的在于提供兩種基于中斷概率約束的MISO竊聽信道魯棒波束成形方法，并且同時考慮沒有人工噪聲輔助和有人工噪聲輔助兩種情況，通過魯棒波束成形設計，能有效地提高通信系統的保密速率，降低竊聽用戶的竊聽能力，提高通信系統的安全性。

為達到上述目的本發明采用如下技術方案：

兩種基于中斷概率約束的MISO竊聽信道魯棒波束成形方法，針對發射機獲取的合法用戶瞬時信道狀態信息非理想，并且發射機僅有竊聽用戶的統計信道狀態信息；

沒有人工噪聲輔助的情況下，利用二分法、半定松弛和Bernstein-type不等式把帶有中斷概率約束的非凸問題轉化為一系列的半定規劃問題，從而得到最優魯棒波束成形方法；

有人工噪聲輔助的情況下，總發射功率被分成有用信號和人工噪聲兩部分，采用一系列數學轉化方法將帶有中斷概率約束的非凸問題轉化為半定規劃問題，獲得有用信號魯棒波束成形以及人工噪聲協方差矩陣的優化設計方法。

進一步，沒有人工噪聲輔助的情況下，具體步驟如下：

對于沒有人工噪聲輔助的情況，發送信號x表示為

x＝ws， (5)

其中，s為發射機向合法用戶發送的符號，E{|s|²}＝1；w為波束成形向量；

在此情況下信干噪比為信噪比，合法用戶和第k個竊聽用戶接收處的信噪比分別為

其中，和分別為合法用戶和第k個竊聽用戶的信道矩陣；(·)^H表示共軛轉置；

沒有人工噪聲輔助的情況下，具體的最大化保密速率問題如下：

其中，P為傳輸功率；R為保密速率；p_k∈(0,1]為允許的最大中斷概率；

第一步：優化問題的轉化

式(7)是一個以傳輸功率P為參數，最大化保密速率R的優化問題，將其轉化為問題(8)；

式(8)是以保密速率R為參數，最小化傳輸功率P的優化問題；

利用如表1所示二分法，通過不斷調整R值解式(8)的問題獲得最優的R^opt，R^opt即為問題(7)的最優解；

表1二分法

假設發射機獲取合法用戶非理想的瞬時信道狀態信息：

其中，為合法用戶信道的估計值；為估計誤差；

此外，假設發射機獲得竊聽用戶的統計信道狀態信息：

其中，為竊聽信道協方差系數。

將式(2)和式(3)代入式(8)，令W＝ww^H，得到其具體形式：

第二步：半定松弛

利用半定松弛，放松W秩為1的條件，將式(9)的問題進一步表示為如下形式：

第三步：利用Bernstein-Type不等式將概率約束轉化為確知形式

令其中，定義式(10)的問題的約束條件表示為

其中，

Bernstein-Type不等式引理：令G＝x^HAx+2Re{x^Ha}，其中，為復Hermitian矩陣。對于任意σ≥0，

其中，s^-(A)＝max(λ_max(-A),0)，λ_max(-A)表示矩陣A最大的特征向量；

利用Bernstein-Type不等式，式(11)可以轉化為如下確知形式：

其中，σ_k＝-ln(p_k)；利用半定松弛后的式(10)的問題通過借助Bernstein-Type不等式最終被轉化為如下半定規劃問題：

其中，μ_k和υ_k為松弛變量；式(13)的問題為凸問題，利用數學工具CVX解得最優W；由于利用半定松弛將W的秩為1的條件進行放松，因此當求解式(13)的問題后得到W不滿足秩為1的條件時，用特征值分解的方法找出W最大特征值對應的特征向量w作為近似的最優波束成形向量。

進一步，有人工噪聲輔助的情況下，MISO竊聽信道魯棒波束成形方法具體步驟如下：

對于有人工噪聲輔助的情況，發送信號x表示為

x＝ws+z， (14)

其中，為添加的人工噪聲向量；

在該情況下，合法用戶和第k個竊聽用戶接收處的信干噪比分別為

其中，和分別為合法用戶和第k個竊聽用戶的信道矩陣；W＝ww^H，Q_z＝zz^H；

此時，最大化保密速率問題具體表示為

Tr(W+Q_z)≤P，W＞＝0，Q_z＞＝0，rank(W)＝1, (16)

其中，P為傳輸功率；R為保密速率。由于式(16)的問題非凸，通過數學轉化將其變為凸問題求解；

第一步：概率約束轉化為確知區域約束

考慮Δh和g_k為獨立高斯分布，不定區域表示為

其中，r_b，r_e,k是不定區域的大小；因此，這一事件以概率1-p_k發生在不定區域如下式所示，確知區域約束是概率約束的充分條件，

因此，問題(16)近似轉化為問題(19)，

其中，Φ^-1(x)為自由度是2N_t的卡方分布的逆累積密度函數，問題(19)的任意可行解也是問題(16)的可行解；

第二步：半定松弛和Charnes-Cooper轉化

經過半定松弛后，放松W秩為1的條件，式(19)轉化為如下最差情況下最大化保密速率的問題：

由于Δh和g_k獨立，式(20)的問題等價于

令W＝S/ξ，Q_z＝Z/ξ，ξ>0，引入松弛變量β利用Charnes-Cooper轉化，式(21)的問題表示為

利用log函數的單調性，式(22)等價轉化為

式(23)可進一步轉化為

其中，τ>0；

第三步：S-procedure轉化

利用S-procedure，式(24)轉化為

其中，Α＝S+Z，Σ＝S-(β-1)Z；λ_h，λ_m，λ_g為松弛變量；若固定β，則上述問題為半定規劃問題，利用CVX工具進行求解；

第四步：一維搜索找到合適的β值

由于R>0，有

進一步推得

由式(22)可知β≥1；所以，一維搜索問題表示為

其中，f(β)表示固定β后問題(25)的最優解τ^opt，其對應的W值即為最優的W；在求得最優的W后，當矩陣W不滿足秩為1的條件時，再次利用特征值分解的方法求得近似的最優波束成形向量w。

本發明在沒有人工噪聲輔助的情況下，利用二分法，半定松弛和Bernstein-type不等式把帶有中斷概率約束的非凸問題轉化為一系列的半定規劃問題，從而得到最優魯棒波束成形設計；在有人工噪聲輔助的情況下，總發射功率被分成有用信號和人工噪聲兩部分，通過將帶有中斷概率約束的非凸問題轉化為半定規劃問題，獲得了有用信號魯棒波束成形以及人工噪聲協方差矩陣的優化設計。

本發明是在發射機可以獲取合法用戶的非理想瞬時信道狀態信息以及竊聽用戶的統計信道狀態信息的模型下給出的兩種波束成形方法，有效地提高通信系統的保密速率，降低竊聽用戶的竊聽能力，提高通信系統的安全性。

【附圖說明】

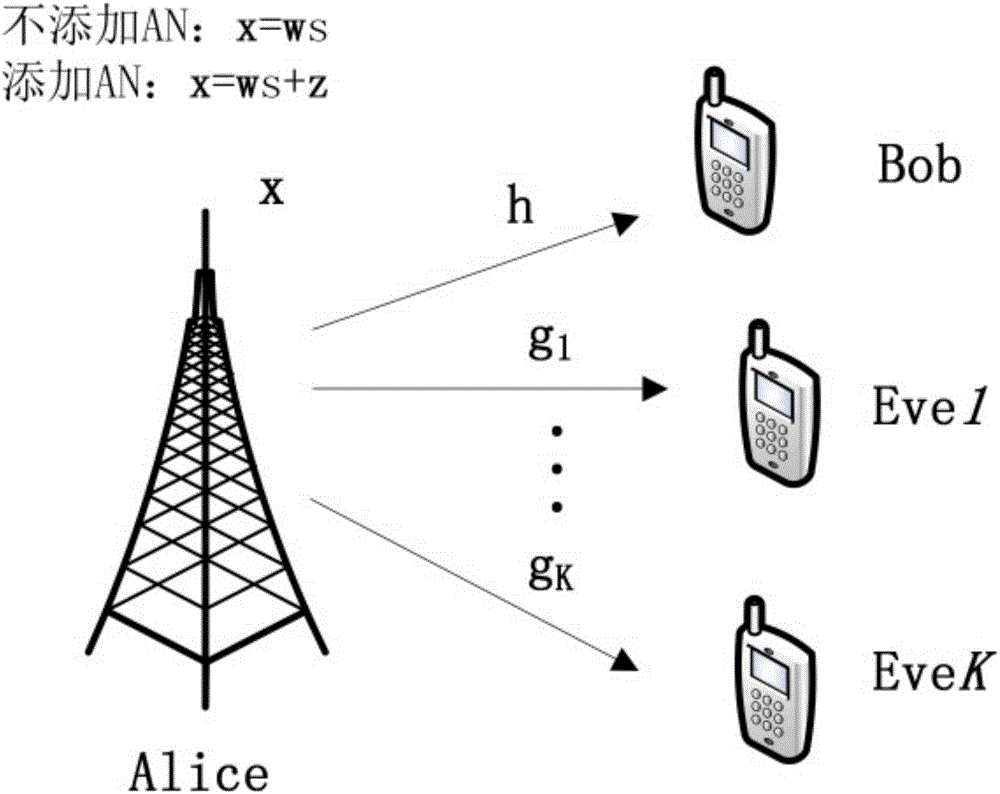
圖1為本發明針對的MISO竊聽信道模型。

【具體實施方式】

下面將結合附圖和實施例對本發明技術方案進行清楚、完整地描述，顯然，所描述的實施例僅是本發明一部分實施例，而不是全部的實施例。基于本發明中的實施例，本領域普通技術人員在沒有作出創造性勞動前提下所獲得的所有其它實施例，都應屬于本發明保護的范圍。

如圖1為本發明針對的MISO竊聽信道模型，包括一個發射機Alice，一個合法用戶Bob，K個竊聽用戶Eve1,…,Eve K。發射機配置N_t根天線，合法用戶和竊聽用戶配置單天線。假設信道為平坦瑞利衰落，將合法用戶和第k個竊聽用戶接收到的信號表示為

其中，為發送信號向量；和分別為合法用戶和第k個竊聽用戶的信道矩陣；不失一般性，分別為合法用戶和第k個竊聽用戶處的加性高斯白噪聲，

本發明在關于合法用戶的瞬時信道狀態信息存在誤差的假設下，進行了具有魯棒性的波束成形設計。假設發射機可以獲取合法用戶非理想的瞬時信道狀態信息：

其中，為合法用戶信道的估計值；為估計誤差。此外，我們假設發射機可以獲得竊聽用戶的統計信道狀態信息：

其中，為竊聽信道協方差系數。

最大化保密速率的優化問題：

本發明嘗試在功率約束和概率約束條件下最大化保密速率：

其中，SINR_b和SINR_e,k分別為合法用戶和第k個竊聽用戶接收端信干噪比；P為傳輸功率；R為保密速率；p_k∈(0,1]為允許的最大中斷概率。

本發明針對發射機獲取的合法用戶瞬時信道狀態信息非理想，并且發射機僅有竊聽用戶的統計信道狀態信息這種情況分別優化魯棒波束成形方案。

①在沒有人工噪聲輔助的情況下，利用二分法，半定松弛和Bernstein-type不等式把帶有中斷概率約束的非凸問題轉化為一系列的半定規劃問題，從而得到最優魯棒波束成形設計(以下稱方案①)；

②在有人工噪聲輔助的情況下，總發射功率被分成有用信號和人工噪聲兩部分，通過一系列數學轉化將帶有中斷概率約束的非凸問題轉化為半定規劃問題，獲得有用信號魯棒波束成形以及人工噪聲協方差矩陣的優化設計(以下稱方案②)。

下面，我們對如何進行魯棒波束成形設計進行詳細介紹。

一：沒有人工噪聲輔助的魯棒波束成形方案

對于沒有人工噪聲輔助的情況，發送信號x表示為

x＝ws， (5)

其中，s為發射機向合法用戶發送的符號，E{|s|²}＝1；w為波束成形向量；

在此情況下信干噪比為信噪比，合法用戶和第k個竊聽用戶接收處的信噪比分別為

其中，和分別為合法用戶和第k個竊聽用戶的信道矩陣；(·)^H表示共軛轉置；

沒有人工噪聲輔助的情況下，具體的最大化保密速率問題如下：

其中，P為傳輸功率；R為保密速率；p_k∈(0,1]為允許的最大中斷概率；

第一步：優化問題的轉化

式(7)是一個以傳輸功率P為參數，最大化保密速率R的優化問題，將其轉化為問題(8)；

式(8)是以保密速率R為參數，最小化傳輸功率P的優化問題；

利用如表1所示二分法，通過不斷調整R值解式(8)的問題獲得最優的R^opt，R^opt即為問題(7)的最優解；

表1二分法

假設發射機獲取合法用戶非理想的瞬時信道狀態信息：

其中，為合法用戶信道的估計值；為估計誤差；

此外，假設發射機獲得竊聽用戶的統計信道狀態信息：

其中，為竊聽信道協方差系數；

將式(2)和式(3)代入式(8)，令W＝ww^H，得到其具體形式：

第二步：半定松弛

半定松弛放松問題(9)中W秩為1的條件，將其轉化為問題(10)；

第三步：利用Bernstein-Type不等式將概率約束轉化為確知形式

令其中，定義問題(10)的概率約束條件表示為

其中，

利用Bernstein-Type不等式，式(11)轉化為如下確知形式：

其中，σ_k＝-ln(p_k)，利用半定松弛后的式(10)的問題通過借助Bernstein-Type不等式最終被轉化為如下半定規劃問題：

其中，μ_k和υ_k為松弛變量；式(13)的問題為凸問題，利用數學工具CVX解得最優W；由于利用半定松弛將W的秩為1的條件進行放松，因此當求解式(13)的問題后得到W不滿足秩為1的條件時，用特征值分解的方法找出W最大特征值對應的特征向量w作為近似的最優波束成形向量。

下面講波束成形向量w獲得的具體實施步驟：

步驟一：

選擇終止參數ε>0，下界R_l和上界R_u令最優解R^opt∈[R_l,R_u]，并且令R_mid＝(R_l+R_u)/2；

步驟二：

將R＝R_mid代入最終轉化的半定規劃問題(13)，解出波束成形向量w，并將解出的w代入問題(8)的概率約束條件檢驗是否滿足；

步驟三：

驗證條件||w||²≤P是否滿足。如果滿足，令R_l＝R_mid；否則令R_u＝R_mid；

步驟四：

如果R_u-R_l≤ε則終止，否則轉到步驟二。

二：有人工噪聲輔助的魯棒波束成形方案對于有人工噪聲輔助的情況，發送信號x表示為

x＝ws+z， (14)

其中，為添加的人工噪聲向量；

在該情況下，合法用戶和第k個竊聽用戶接收處的信干噪比分別為

其中，和分別為合法用戶和第k個竊聽用戶的信道矩陣；W＝ww^H，Q_z＝zz^H；

此時，最大化保密速率問題具體表示為

Tr(W+Q_z)≤P，W＞＝0，Q_z＞＝0，rank(W)＝1,

(16)其中，P為傳輸功率；R為保密速率，由于式(16)的問題非凸，通過數學轉化將其變為凸問題求解；

第一步：概率約束轉化為確知區域約束

如下式所示，確知區域約束是概率約束的充分條件，

因此，問題(16)近似轉化為問題(19)，

其中，Φ^-1(x)為自由度是2N_t的卡方分布的逆累積密度函數，問題(19)的任意可行解也是問題(16)的可行解；

第二步：半定松弛和Charnes-Cooper轉化

半定松弛放松W秩為1的條件，式(19)轉化為如下最差情況下最大化保密速率的問題：

由于Δh和g_k獨立，式(20)的問題等價于

令W＝S/ξ，Q_z＝Z/ξ，ξ>0，引入松弛變量β利用Charnes-Cooper轉化，式(21)的問題表示為

利用log函數的單調性，式(22)等價轉化為

式(23)可進一步轉化為

其中，τ>0；

第三步：S-procedure轉化

利用S-procedure，式(24)轉化為

其中，Α＝S+Z，Σ＝S-(β-1)Z；λ_h，λ_m，λ_g為松弛變量；若固定β，則上述問題為半定規劃問題，利用CVX工具進行求解；

第四步：一維搜索找到合適的β值

一維搜索問題表示為

其中，f(β)表示固定β后問題(25)的最優解τ^opt，其對應的W值即為最優的W；在求得最優的W后，當矩陣W不滿足秩為1的條件時，再次利用特征值分解的方法求得近似的最優波束成形向量w。下面講波束成形向量w獲得的具體實施步驟：

步驟一：

確定β的范圍為步長為1，從β＝1到按步長將不同的β值入代問題(25)求得不同的τ值；

步驟二：

找出其中最大的τ值即為最優的τ^opt；

步驟三：

找出τ^opt對應的β值，將此β值再次代入問題(25)解出W和Q_z；

步驟四：

在求得W后，當矩陣W不滿足秩為1的條件時，我們再次利用特征值分解的方法求得近似的最優波束成形向量w。

至此，我們詳細描述了本發明的具體實施例。

以上所述是本發明的優選實施方式，通過上述說明內容，本技術領域的相關工作人員可以在不偏離本發明技術原理的前提下，進行多樣的改進和替換，這些改進和替換也應視為本發明的保護范圍。