本發明涉及深基坑支護工程技術領域，特別是指一種長短樁組合支護結構計算方法。

背景技術：

在深厚軟土地區的基坑支護設計過程中，為了保證基坑的整體抗滑移穩定、抗隆起穩定及抗傾覆穩定等要求，基坑支護樁需要穿過深厚軟土進入下覆性能較好的地層，支護樁的樁長主要由軟土層下覆穩定地層的埋深確定，與基坑的開挖深度關系不大，在這種情況下，當基坑開挖深度加深時，支護設計一般只需調整支護樁的樁徑、樁身的配筋及外加的水平內支撐的層數，支護樁的樁長變化不大。由此造成的結果是：對于開挖深度7～10m左右的中等深度的基坑，其支護樁長度在20m以上，甚至達到30多米，大大地增加了基坑支護的造價，極度浪費了國家和社會的資源，與當今全社會提倡的低碳環保理念背道而馳。

采用長短樁組合支護結構，既能節省鋼筋、混凝土、水泥等建筑材料的用量，又能節省工期，從而為建設方節省投資，減少資源浪費，達到低碳環保、節能減排的目標。

技術實現要素：

本發明針對深厚軟土地區基坑工程中支護樁樁長過長且相鄰的支護樁樁長一致而造成社會資源極大浪費的現狀，提供一種長短樁組合支護結構計算方法，該方法適用于任意地層和工況，在深厚軟土地層經濟效益尤其顯著。

本發明所采用的技術方案是：

一種長短樁組合支護結構的計算方法，包括以下步驟：

步驟1，沿基坑壁依次間隔布置若干長支護樁區和短支護樁區，所述長支護樁區由多根長支護樁構成，所述短支護樁區由多根短支護樁構成，所述長支護樁和短支護樁的樁頂由冠梁連接；

步驟2，局部單元模型的選取。對長短樁組合支護結構進行設計時，為提高效率，可根據支護樁平面布置的方式，選擇最薄弱和危險區段的若干根長短樁作為局部單元模型進行分析計算。所述的最薄弱和危險區段為(n_i-1+m_i+n_i)/m_i數值最大的區段，包括長、短支護樁和部分冠梁。其中m_i表示第i個長支護樁區長支護樁的根數，n_i表示第i個短支護樁區短支護樁的根數，第i-1個短支護樁區和第i個短支護樁區分別位于第i個長支護樁區的兩側。

步驟3，計算模型的簡化。對選定的局部單元模型，短支護樁樁底以上部分的土壓力由長支護樁、短支護樁共同承擔，單根支護樁承擔的土壓力計算寬度L₁為樁間距s，短支護樁樁底以下部分的土壓力完全由長支護樁獨立承擔，單根支護樁承擔的土壓力計算寬度L₂即為(0.5n_i-1+m_i+0.5n_i)/m_i倍的樁間距；假定樁頂部分冠梁相對支護樁為完全剛性。

步驟4，控制方程的建立。對選定的局部單元模型中的單根支護樁，根據彈性抗力法的理論，其控制方程為：

其中，為支護樁長；

為沿支護樁深度，以開挖方向為正；

w為樁身側向位移，以朝基坑方向為正；

E_p為樁身彈性模量；

I_p為樁身截面慣性矩；

被動區沿樁身的地基梁的反力系數，根據場地條件按相關規范確定；

為主動區樁身荷載分布，根據實際條件按相關規范確定；

對于多土層情況，在單層土中重復上述控制方程。

步驟5，邊界條件的設置。上述單根支護樁的控制方程是一元四次非齊次常微分方程，與樁頂和樁底邊界處的四個邊界條件，構成了閉合的邊值問題，求解該邊值問題可以得到沿樁身的位移、轉角、剪力和彎矩，從而用于支護樁的設計。對于單根支護樁，所述的控制方程的求解需要4個邊界條件；同樣地，對于選定的含N_p根支護樁的局部單元模型，其控制方程組的求解總共需要4N_p個邊界條件，其中N_p＝n_i-1+m_i+n_i。

對于選定的含N_p根支護樁的局部單元模型，可假定各支護樁樁底的彎矩和剪力均為零，構成2N_p個邊界條件；因冠梁在平面外的抗彎能力很差，無法提供抗彎彎矩，可假定各支護樁樁頂的彎矩為零，構成N_p個邊界條件；因局部單元模型中各支護樁的空間位置接近，冠梁相對支護樁為完全剛性，可假定各支護樁的樁頂位移相同，構成N_p-1個邊界條件；此外，可假定局部單元模型中的冠梁處于平衡狀態，局部單元模型的樁頂反力構成平衡，構成1個邊界條件。上述的基本假定合計構成4N_p個邊界條件，與含N_p根樁的局部單元模型的N_p個控制方程構成閉合的邊值問題。

步驟6，邊值問題的打靶算法求解。在實際工程中，對于上述局部單元模型的控制方程組，很難得到其完全解析解，即使得到解析解，工程使用也不方便，意義不大。本發明提出一種基于布羅伊登迭代法的打靶算法針對該問題進行快速求解。該算法只需要少數迭代即可收斂，且對初值的設置并不敏感，具有良好的收斂性。

打靶算法的核心思想是將邊界問題轉化為初值問題，然后基于初值問題進行迭代求解，因為初值問題的求解較為簡單。對于選定的含N_p根樁的局部單元模型，選擇各支護樁樁頂的N_p個轉角、1個共同的樁頂位移以及其中N_p-1根樁的樁頂剪力為未知量，通過初值問題的求解，構造出以樁底的剪力和彎矩為因變量的“打靶”函數；以各支護樁樁底的彎矩和剪力均為零的2N_p個邊界條件為“靶的”，構建打靶代數方程；采用布羅伊登迭代法求解代數方程，得到滿足樁底剪力和彎矩邊界條件的樁頂位移、轉角及剪力的未知量；以樁頂解為初始條件，再次求解初值問題，獲得支護樁沿深度的位移、轉角、彎矩和剪力。整個求解過程類似“打靶”，所以該求解方法又稱為打靶算法。

與現有技術相比，本發明具有以下優點：

該計算方法考慮了長短樁的一般布置方式，具有良好的通用性；提出了局部單元模型的概念，只需對最危險區域進行計算，不需要對結構進行整體分析，在滿足設計安全性的同時，能夠考慮長短樁組合結構共同作用的空間效應，包括土壓力的分擔、冠梁的協同作用等，計算模型簡單，物理概念明確；本計算方法依托彈性抗力法，能夠與多層土體系、多工況的彈性抗力法相結合，與當前規范直接接軌，針對性強，適用范圍廣；方程求解采用了布羅伊登迭代法，是針對多未知數的多維條件下的割線算法，在迭代過程中采用雅各比猜測矩陣，對初值的設置并不敏感，收斂速度快，穩定性好。

附圖說明

圖1為長短樁組合支護結構的平面布置示意圖。

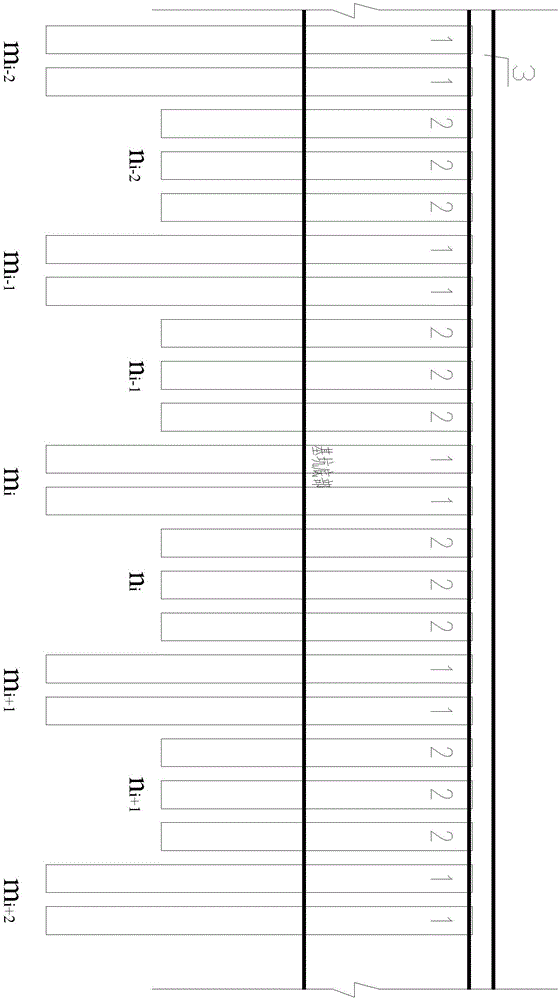
圖2為長短樁組合支護結構的立面圖。

具體實施方式

為了使本發明的上述目的、特征和優點能夠更加明顯易懂，下面結合附圖對本發明的具體實施方式做詳細的說明。

根據圖1、圖2所示，一種長短樁組合支護結構的計算方法，沿基坑壁依次間隔布置若干長支護樁區和短支護樁區，每個長支護樁區由2根長支護樁1構成，每個短支護樁區由3根短支護樁2構成，長支護樁1和短支護樁2的樁頂由冠梁3連接；

選擇圖1中線框內的8根支護樁作為最薄弱和危險的局部單元模型進行分析計算，短支護樁2樁底以上部分的土壓力由長支護樁1、短支護樁2共同承擔，單根樁承擔的土壓力計算寬度L₁即為樁間距s，短支護樁2樁底以下部分的土壓力完全由長支護樁1獨立承擔，單根支護樁承擔的土壓力計算寬度L₂，即為2.5倍的樁間距。

對選定的局部單元模型中的8根單根樁，根據彈性抗力法的理論，其控制方程為

其中，為支護樁長；

為沿支護樁深度，以開挖方向為正；

w為樁身側向位移，以朝基坑方向為正；

E_p為樁身彈性模量；

I_p為樁身截面慣性矩；

被動區沿樁身的地基梁的反力系數，根據場地條件按相關規范確定；

為主動區樁身荷載分布，根據實際條件按相關規范確定；

對于多土層情況，在單層土中重復上述控制方程，對于多工況情況，按規范修改相應的和

對于選定的含8根樁的局部單元模型，假定各樁樁底的彎矩和剪力均為零，構成16個邊界條件；假定各樁樁頂的彎矩為零，構成8個邊界條件；假定各樁的樁頂位移相同，構成7個邊界條件；假定局部單元模型中的冠梁處于平衡狀態，局部單元模型的樁頂反力平衡，構成1個邊界條件。上述假定合計構成32個邊界條件，與描述8根樁的8個彈性抗力法控制方程，構成閉合的邊值問題。

選擇各樁樁頂的8個轉角、1個共同的樁頂位移以及其中7根樁的樁頂剪力為未知量(另外一根樁樁頂的剪力可由平衡方程確定)，假設這16個未知數可由矢量J集中地表示，那么局部單元中各樁的初始條件可以由J表示，見表一：

表一各樁樁頂的初始條件

其中第8根樁的樁頂反力，由平衡方程可以得到：

基于表一中的初始條件，可對每根樁的控制方程單獨進行積分，構造出以J為自變量、以樁底的剪力和彎矩為因變量的函數：

F＝f(J) (3)

該函數即為打靶函數。以各樁樁底的彎矩和剪力均為零的16個邊界條件為“靶的”，建立打靶代數方程：

f(J)＝0 (4)

通過布羅伊登法迭代算法對式(4)中的16元代數方程進行求解，尋找滿足樁底剪力和彎矩邊界條件的樁頂位移、轉角及剪力J^*，即

f(J^*)＝0 (5)

將J^*再次代入表一得到真實的樁頂初始條件，并對控制方程組進行積分，即可得到支護樁樁身的位移、轉角、彎矩和剪力。布羅伊登算法迭代求解方程(4)的流程見表二：

表二布羅伊登法迭代求解基本流程表

本發明提出一種基于布羅伊登法迭代的打靶算法只需要幾次迭代即可收斂，對初值的設置并不敏感，在迭代過程中不直接采用雅各比矩陣，而是采用雅各比猜測矩陣進行代替，收斂速度快，穩定性好。

說明書中未闡述的部分均為現有技術或公知常識。本實施例僅用于說明該發明，而不用于限制本發明的范圍，本領域技術人員對于本發明所做的等價置換等修改均認為是落入該發明權利要求書所保護范圍內。