本發明涉及一種基于UG和MATLAB的多自由度注塑機械臂建模方法，屬于機器人路徑優化
技術領域：
。
背景技術：
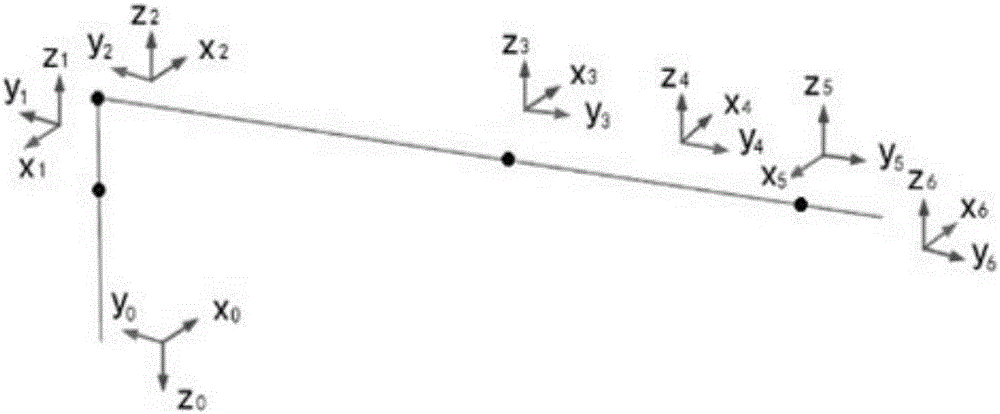
：針對多自由度注塑機械臂系統在有限空間約束條件下作高效兩點重復運動，在滿足機械臂性能的情況下，使系統在最短時間完成給定負載兩點間抓運工作，提高生產效率，軌跡規劃成為系統控制的關鍵問題。文獻(于天宇，李達，宋寶玉.基于MATLAB-Robotics工具箱的工業機器人軌跡規劃及仿真研究[J].機械工程師，2011(7):81-83)利用D-H參數法建立機器人模型，通過調用MATLABRobotics工具箱函數進行機器人運動學正反解運算，運用多項式插值擬合機器人運動軌跡曲線，對機器人多個關節軌跡進行規劃和仿真；文獻(李輝，黃文權，李開世.基于復雜路徑下的六自由度機器人動力學仿真[J].機械設計與制造，2015(9):208-210)將Adams建立的機械臂導入Matlab中，利用Simulink仿真模塊搭建聯合仿真系統，實現機械系統與控制系統的聯合仿真，但這種方法在復雜環境下可能由于干涉情況和運動策略考慮不夠全面而無解。總體來說，當前國內外的研究主要集中在無約束或者前約束條件下生成和優化機械臂的運動軌跡，也有學者將機械臂的運動學性能、動力學性能和特殊的工作條件(如：運動時間、生產效率、運動空間等)等與機械臂軌跡規劃相結合進行研究。在有限空間約束條件下，針對機械臂的軌跡規劃化問題，基于結構動力學和控制系統運動學的協同仿真方法還未有文獻記載。技術實現要素：本發明要解決的技術問題是：針對多自由度注塑機械臂在有限空間約束條件下的軌跡規劃問題，提供一種基于UG和MATLAB的多自由度注塑機械臂建模方法，建立了機械臂關節空間運動軌跡方程，將運動時間、生產效率、運動空間等進行約束，得到了一條滿足實際工況要求的最優軌跡。本發明采取的技術方案為：一種基于UG和MATLAB的多自由度注塑機械臂建模方法，該方法包括以下步驟：(1)采用UG對多自由度注塑機械臂建立參數化驅動的模型；(2)建立傳遞函數為M函數，M函數以機械臂的運動參數與控制參數為輸入，以機械臂在有限空間的運動軌跡為輸出；(3)通過設定GUI參數和修改傳遞文件，將M函數傳遞給UG運用MATLABRoboticsToolboxlink函數建立機械臂運動學模型，并在MATLAB中建立機械臂控制系統運動學方程；(4)在MATLAB中驅動函數得到機械臂各關節位姿，調用drivebot函數可調節控制界面的滑條轉動各關節，觀察機械臂在空間中運動的軌跡、范圍；(5)將UG作為MATLAB/Simulink中的運動分析計算引擎，實時提供機械臂在當前運動參數和控制參數下的運動分析，根據當前運動情況計算下一時刻機械臂的運動參數和控制參數，將MATLAB/Simulink的控制系統模塊嵌入到UG中，在每個時間迭代步，計算機械臂的實時運動參數以確定最優軌跡，在協同仿真模式下，NX和MATLAB/Simulink的仿真條件根據當前系統運行條件解算確定。步驟(9)中，在不考慮摩擦力等外界干擾的作用，機械臂的動力學方程為：D(q)q··+C(q,q·)q·+G(q)=τ---(8)]]>式中：D(q)—n×n階對稱正定的慣量矩陣；—n×n階離心力和哥氏力項；G(q)—重力項。基于M函數的Simulink控制器與機械臂的仿真模型函數關系式為：τ=f0(q··d,q·d,qd,q,q·)---(9)]]>q··=f1(q,q·,τ)---(10)]]>式中：τ—控制器輸出與受控對象輸入的關節驅動力矩/力，q—關節的角速度和角位移；qd—期望關節軌跡的角加速度，角速度和角位移。D(q)=P1+P2+P3+2P4cosq3P2+P3+P4cosq3P3+P4cosq3P2+P3+P4cosq3P3+P4cosq3P4cosq3P3+P4cosq3P4cosq3P3]]>C(q,q·)=-2P4q·3sinq3-P4q·3sinq3-P4q·3sinq3P4q·2sinq3P4q·2sinq3P4q·2sinq3P4q·1sinq3P4q·1sinq30]]>G(q)=P5gcosq1+P6gcos(q1+q2)+P7gcos(q1+q2+q3)+P8gcos(q1)P6gcos(q1+q2)+P7gcos(q1+q2+q3)P7gcos(q1+q2+q3)]]>P＝[P1,P2,P3,P4,P5,P6,P7,P8]為線性后的參數向量式中：P1＝I1+m1r12+(m2+m3)l12；P2＝I2+m2r22+m3(l1+l2)2；P3＝I3+m3r32；P4＝m2r2l1+m3r3(l1+l2)；P5＝m1r1；P6＝m2r2；P7＝m3r3；P8＝(m2+m3)l1；g—重力加速度。本發明的有益效果：與現有技術相比，本發明效果如下；(1)通過協同仿真，以結構動力學和控制系統運動學協同仿真相結合為途徑，尋求在有限空間約束下機械臂軌跡優化方法，實現了優化后軌跡關節平滑驅動；(2)因多自由度機械臂系統動力學模型高度復雜，耦合性強，具有非線性時變性，運用結構動力學和控制系統運動學協同仿真規劃機械臂軌跡精確性高，并采用M函數的機械臂控制系統建模仿真，通用性強，是一種簡單可靠、行之有效的機械臂控制系統仿真方法；(3)以有限空間為約束條件，在機械臂軌跡優化的仿真過程中，通過M函數設定的參數按某種規律變化的時變參數，規劃過程中的關節角變化、運動時間優化和末端軌跡優化等，波動小，計算穩定，收斂迅速。附圖說明圖1是有限空間約束條件下注塑機械臂模型；圖2是注塑機械臂D-H坐標系；圖3是注塑機械臂運動路徑(A：起點，B：終點)圖4是注塑機械臂協同仿真前長臂關節運動軌跡；圖5是注塑機械臂協同仿真前末端運動軌跡；圖6是注塑機械臂關節角變化曲線；圖7是機械臂協同仿真機制原理；圖8是NX嵌入MATLAB/Simulink具體實現流程；圖9是控制系統協同仿真結構圖；圖10是注塑機械臂末端軌跡擬合曲線；圖11是注塑機械臂協同仿真長臂關節運動軌跡圖；圖12是注塑機械臂協同仿真末端運動軌跡圖。具體實施方式下面結合附圖及具體的實施例對本發明進行進一步介紹。實施例1：一種基于UG和MATLAB的多自由度注塑機械臂建模方法，該方法包括以下步驟：(1)對多自由度注塑機械臂建模：首先對機械臂的模型進行簡化，運用UG三維軟件建立機械臂三維模型，通過表達式驅動其尺寸變化，將模型尺寸存儲數據庫，任意修改、增加數據或設計變量，模型自動同步更新，實現表達式驅動機械臂長臂建模，有限空間約束條件下機械臂在有限空間運動軌跡示意圖，如圖1所示，圖中，A、B：注塑機；C：機械臂；D：傳輸帶；表1表達式驅動機械長臂建模參數名稱計算公式計算值P0100100P1＝6*p0600P2＝6*p0/p12(2)建立注塑機械臂動力學模型：在有限空間約束的條件下，根據步驟(1)中的機械臂模型，建立機械臂的D-H空間坐標系(如圖2所示)和D-H參數，如表2所示，D-H空間坐標系包括系統全局坐標系和關節坐標系；表2機械臂D-H參數表(3)根據機械臂末端的位置和方位，將笛卡爾空間映射到關節空間，求得機械臂的自由運動空間和各關節變量；機械臂的控制需要在確定末端姿態的情況下，求解各個關節的變量值。通過運動學分析，得到機械臂末端位姿矩陣：P=T60-T10(θ1)T21(θ2)T32(θ3)T43(θ4)T54(θ5)T65(θ6)=nxoxaxpxnyoyaypynzozazpz0001]]>工作空間決定機械臂的末端位置，θ1-θ6為相對起點的轉動角度，通過逆運動學分析求解θ1,θ2,θ3,θ4,θ5,θ6[7].θ1=arctan2(Px,Py)-arctan2(d2,±Px+Py-d22)---(1)]]>θ3=arctan2(a3,d4)-arctan2(k,±a32+d42-k2)---(2)]]>其中：k=px2+py2+pz2-a22-a32-d22-d422a2]]>式中，正、負號對應的兩個解對應于θ1的兩個可能解。θ23=θ2+θ3=arctan2[-(a3+a2c3)Pz(c1Px+s1Py)+(a2s3-d4)(-d4+a2c3)Pz+(c1Px+s1Py)(a2s3+a3)],---(3)]]>θ2＝θ23-θ3(4)θ4＝arctan(-axs1+ayc1,-axc1c23-ays1c23+azs23)(5)θ5＝arctan2(s5,c5)(6)其中：s5＝-ax(c1c23c4+s1s4)-ay(s1c23c4-c1s4)+az(s23c4)c5＝ax(-c1s23)+ay(-s1s23)+az(-c23)θ6＝arctan2(s6,c6)(7)其中：s6＝-nx(c1c23c4-s1c4)-ny(s1c23s4+c1c4)+nz(s23s4)c6＝nx[(c1c23c4+s1s4)c5-c1s23s5]+ny[(s1c23c4-c1s4)c5-s1s23s5]-nz(s23c4c5+c23s5)式中：Si,Ci—第i(i＝1,2,…,6)個關節正弦值和余弦值。(4)通過MATLABRoboticsToolbox強大的矩陣計算功能，實現基于MATLAB的智能機械臂空間軌跡運動求解，運用MATLABRoboticsToolboxlink函數建立機械臂模型；上述步驟(4)中MATLABRoboticsToolboxlink函數的link函數如下：L＝link([alphaAthetaDsigma],’CONVENTION’)其中：CONVENTION分為標準的D-H參數的’standard’和改進的D-H參數’modified’；alpha代表扭轉角；A代表桿件長度；theta代表關節角；D代表橫距；sigma代表關節類型：0為旋轉關節，非0為移動關節；(5)在MATLAB中建立機械臂控制系統運動學方程，驅動函數得到機械臂各關節位姿，調用drivebot函數可調節控制界面的滑條轉動各關節，觀察機械臂在空間中運動的軌跡、范圍；(6)根據有限空間約束條件下的實際工況，在滿足機械臂運動范圍、與其它零件沒有干涉和符合工作要求的前提下選擇一條行程最短、能量消耗最小和機械臂空間變換最少的路徑，注塑機械臂運動路徑如圖3所示；(7)調用工具箱中jtral函數生成機械臂的關節軌跡，從而對末端路徑規劃.jtral函數為計算兩點之間關節空間軌跡的函數，在無約束時利用五次多項式插值對速度和加速度進行求解，只要已知初始點與終止點之間的關節角度值即可確定路徑的變化情況，其調用格式為[qqdqdd]＝jtral(qz,qr,t)，其中，qz：初始點的關節角度值，qr：終止點的關節角度值，t：初始點運動到終止點時的運行時間。利用運動學正解函數T＝fkine(rbt,q)求得機械臂初始、終止位置狀態的齊次變換矩陣；初始位置角度：qz＝[0,0,0,0,0,0]，位姿矩陣如下所示：T=1.0e+003*0.0010001.100000.00000.001000-0.00100.00000.30000000.0010]]>終止位置角度：qz＝[pi/2,-pi/13,pi/7,0,pi/6,0]，位姿矩陣如下所示：T=1.0e+003*-0.0005-0.0000-0.0009-0.05000.0008-0.0002-0.00051.0588-0.0002-0.00100.00010.34350000.0010]]>(8)逆向運動求解，由機械臂終止位置各個關節位姿，取機械臂各關節離散點，通過對所取的離散點進行連續求逆，得到θ1-θ6對應的六關節的角轉動變量。機械臂6個關節所對應的部分轉角，機械臂6個關節所對應的部分轉角，如表3所示，圖4、圖5所示分別為協同仿真前長臂和末端運動軌跡圖，圖6所示為機械臂各關節變化曲線；表3機械臂各關節所對應的部分轉角(9)將UG作為MATLAB/Simulink中的運動分析計算引擎，實時提供機械臂在當前運動參數和控制參數下的運動分析，根據當前運動情況計算下一時刻機械臂的運動參數和控制參數，將MATLAB/Simulink的控制系統模塊嵌入到UG中，在每個時間迭代步，計算機械臂的實時運動參數以確定最優軌跡，在協同仿真模式下，NX和MATLAB/Simulink的仿真條件根據當前系統運行條件解算確定，因此該方法與實際工況更加符合，仿真的準確度與置信度更高。協同仿真機制與機械臂控制系統設計相結合，其原理，如圖7所示；步驟(9)中，UG嵌入MATLAB/Simulink時，在UG運動仿真模塊設定仿真接口，將處理與UG接口的全部操作編譯成獨立的M函數，該M函數嵌入到MATLAB/Simulink模塊的動態系統仿真模型中，編譯的M函數以機械臂的運動參數與控制參數為輸入，以機械臂在有限空間的運動軌跡為輸出，通過設定GUI參數和修改傳遞文件，將M函數傳遞給UG，其協同仿真的具體實現方法，如圖8所示；步驟(9)中，機械臂的動力學方程在不考慮摩擦力等外界干擾的作用時為：D(q)q··+C(q,q·)q·+G(q)=τ---(8)]]>式中：D(q)—n×n階對稱正定的慣量矩陣；—n×n階離心力和哥氏力項；G(q)—重力項。基于M函數的Simulink控制器與機械臂的仿真模型函數關系式為：τ=f0(q··d,q·d,qd,q,q·)---(9)]]>q··=f1(q,q·,τ)---(10)]]>式中：τ—控制器輸出與受控對象輸入的關節驅動力矩/力，q—關節的角速度和角位移；qd—期望關節軌跡的角加速度，角速度和角位移。D(q)=P1+P2+P3+2P4cosq3P2+P3+P4cosq3P3+P4cosq3P2+P3+P4cosq3P3+P4cosq3P4cosq3P3+P4cosq3P4cosq3P3]]>C(q,q·)=-2P4q·3sinq3-P4q·3sinq3-P4q·3sinq3P4q·2sinq3P4q·2sinq3P4q·2sinq3P4q·1sinq3P4q·1sinq30]]>G(q)=P5gcosq1+P6gcos(q1+q2)+P7gcos(q1+q2+q3)+P8gcos(q1)P6gcos(q1+q2)+P7gcos(q1+q2+q3)P7gcos(q1+q2+q3)]]>P＝[P1,P2,P3,P4,P5,P6,P7,P8]為線性后的參數向量式中：P1＝I1+m1r12+(m2+m3)l12；P2＝I2+m2r22+m3(l1+l2)2；P3＝I3+m3r32；P4＝m2r2l1+m3r3(l1+l2)；P5＝m1r1；P6＝m2r2；P7＝m3r3；P8＝(m2+m3)l1；g—重力加速度。機械臂的物理參數：m1＝4.8kg,m2＝2.7kg,m3＝0.7kgl1＝0.6m,l2＝0.4m,l3＝0.1m；r1＝0.3m,r2＝0.2m,r3＝0.05m將M函數文件嵌入到相應模塊中，Simulink中連接各個模塊的連線能夠傳遞向量，由各個模塊組成的系統協同仿真控制系統結構，如圖9所示。其中左側部分為輸入量，右側部分為輸出量；為使機械臂末端軌跡光滑，將得到的軌跡曲線進行擬合，通過對平滑擬合曲線取點得到末端的轉動變量，擬合曲線，如圖10所示。以有限空間為約束條件，在機械臂軌跡優化的仿真過程中，通過M函數設定的參數按某種規律變化的時變參數，規劃過程中的關節角變化、運動時間優化和末端軌跡優化等，波動小，計算穩定，收斂迅速，由此可見，聯合仿真在機械臂軌跡規劃的過程中起到了重要作用，最終得到了滿足實際需求的軌跡近似最優解。協同仿真長臂和抓手關節運動軌跡圖，如圖11、圖12所示。以上所述，僅為本發明的具體實施方式，但本發明的保護范圍并不局限于此，任何熟悉本
技術領域：
的技術人員在本發明揭露的技術范圍內，可輕易想到變化或替換，都應涵蓋在本發明的保護范圍之內，因此，本發明的保護范圍應以所述權利要求的保護范圍為準。當前第1頁1 2 3