本發明涉及油田勘探開發技術領域，特別是涉及到一種基于深變子波的合成記錄制作方法。

背景技術：
：

疊前深度偏移技術的研究是近10多年來全球油氣地球物理勘探領域的熱點，是目前地震資料處理技術中歸位相對準確的一種偏移方法，特別是在速度復雜或者構造復雜地區具有較明顯的優勢，主要用來解決鹽丘、復雜基底、復雜斷塊、生物礁、泥底辟、流體底辟等復雜地質體的波場成像問題。隨著偏移算法的成熟、計算機能力的進步，規模化的疊前深度偏移成為可能。深度域地震剖面與時間域地震剖面相比，具有地下構造真實、直觀、便于解釋等特點，并且無需進行時深轉換就能得到初始深度構造。目前，疊前深度偏移已經是工業界的標準處理流程。因此如何對疊前深度偏移后的地震數據進行后續的井震標定、構造解釋及其它的應用就成為必須面對的問題，并且，制作深度域合成記錄是對疊前深度偏移后的地震數據進行一切后續工作的基礎和關鍵。

張雪建(2000)等認為在時間域合成地震記錄是地震子波與反射系數的褶積，深度域的合成地震記錄也與時間域類似，只不過先要將時間域的子波轉換成深度域的子波；然后利用聲波時差曲線和密度曲線計算出深度域的反射系數,二者褶積便可得到深度域的合成地震記錄。該方法的關鍵在于提取子波和計算反射系數，要在深度偏移剖面上選取品質較好的井旁地震道計算子波的主頻,要選用零相位子波，在計算反射系數之前，要對聲波時差曲線和密度曲線進行校正、去野值等處理。

何惺華(2005)對深度域地震記錄的應用開展了討論，從時間域和深度域的地震波場描述出發，對深度域的子波、褶積和Fourier變換等基本問題進行分析探討。證明了時間域與深度域中的地球物理概念、原理和方法是相互聯系的，其數學表達方式是相似的。對深時轉換中采樣間隔的選擇、頻率譜與波數譜數據的關系和深時轉換剖面上視頻率變化等實際問題，給出了合理的解釋。

王永剛(2005)對深度域的地震資料合成記錄制作方法進行了探討。總結歸納深度域合成記錄制作過程應該包括：(1)利用聲波、密度等測井曲線進行層位劃分建立深時關系，根據多層介質反射系數的波動方程推導公式，求取頻率域的反射系數；(2)對時間域的井旁道記錄利用同態反褶積方法提取地震子波，得到頻率域的子波譜；(3)利用頻率域褶積模型計算合成記錄，作反傅里葉變換得到時間域合成地震記錄，再根據時深關系求出每個時域采樣點對應的深度點，按照所要求的深度采樣點間隔進行重采樣，得到深度域合成地震記錄。

林伯香等(2006)認為，諧波在時間域中經過反射系數“系統”后不改變頻率,符合線性時不變系統的條件,因此在時間域中可以用子波與反射系數序列褶積的方法計算時間域合成地震記錄。由于在深度域中子波的波數隨介質速度變化,因此地震子波在深度域中傳播并不滿足線性時不變系統的條件,不能直接用褶積的方法計算深度域合成地震記錄。林伯香等利用簡單的理論模型,通過對深度域中的速度、深度參數進行適當的變換,使其在新深度域中符合線性時不變系統的條件,在保證層間旅行時不變的情況下,定義深度域地震子波的介質速度為標準速度，將其他各層的速度都以標準速度進行調整,并對層間厚度也做相應的調整。通過上述變換,可把時間域中的計算方法引用到深度域中,再通過反變換處理,將新深度域中的褶積結果反變換到原深度域中。如果不考慮深度域與時間域之間的重采樣誤差,常規時間域合成地震記錄經時深轉換到深度域后的結果應該與深度域合成地震記錄結果一致。

以上方法都沒有考慮到當密度曲線欠缺時，如何根據實際情況由速度曲線轉換得出密度曲線，并且當欠缺密度曲線時，一味地使用Gardner公式來轉換，準確率太低。另外，在深度域，子波在某一時刻的傳播長度受地層速度的影響，子波的長度隨著速度的變化而變化，是地層速度的函數，不是固定值，這就給深度域合成記錄的制作帶來困難。

為此我們發明了一種新的基于深變子波的合成記錄制作方法，解決了以上技術問題。

技術實現要素：
：

本發明的目的是提供一種可以根據具體的沉積相態得到更合理的密度曲線，從而大大提高了深度域合成記錄制作的準確率的基于深變子波的合成記錄制作方法。

本發明的目的可通過如下技術措施來實現：基于深變子波的合成記錄制作方法，該基于深變子波的合成記錄制作方法包括：步驟1，輸入時間域子波、速度曲線和密度曲線，在沒有密度曲線時，不輸入密度曲線；步驟2，建立時間域子波與速度的函數關系，將時間域子波轉換成深度域子波，即生成深變子波；步驟3，在步驟1輸入了密度曲線時，使用速度和密度曲線，計算反射系數；步驟4，將深變子波與反射系數進行褶積，制作深度域合成記錄。

本發明的目的還可通過如下技術措施來實現：

在步驟2中，設定w(t)是時間域雷克子波，w(h)是深度域子波，v(h)是子波在深度h時的傳播速度，計算深度為h時，深度域子波w(h)的形態，

假設，t時刻的時間域子波w(t)與深度h的深度域子波w(h)相對應，t^/時刻的時間域子波w(t^/)相對應的深度域子波是w(h^/)，

若將t與t^/之間的時間平均分成n份，那么時間間隔Δt＝(t^/-t)/n，

假設，時刻t₁＝t-Δt，t₂＝t-2Δt，與t₁時刻對應的深度是h₁，與t₂時刻對應的深度是h₂，那么

如公式1和公式2所述，對于時間域子波w(t)周期T內的任意時刻t^/都可計算出所對應的深度值h^/，從而找準任意時刻的w(t^/)所對應的深度域子波w(h^/)，并且由公式3計算出由于速度變化而時刻改變的深度域子波周期H(v)，

將時間域子波轉換到深度域后，由于速度的影響，波形隨深度發生壓縮或拉伸兩種變化。

在步驟3中，在步驟1沒有輸入密度曲線時，根據陸相沉積環境當中不同沉積相態，給定針對性的擬合公式，計算密度曲線。

在步驟3中，在步驟1沒有輸入密度曲線，只有速度曲線時，首先根據實際工區資料，擬合出比較符合實際的密度曲線，采用的密度與速度的經驗公式是

D＝αv_p^β (公式4)

其中D是密度，v_p是縱波速度，α、β為參數值，根據實際工區，針對α、β做出相應的調整。

在步驟3中，當有真實的速度曲線和密度曲線時，由如下公式得到每一深度的的反射系數：

其中R_i是第i層與第i+1層界面的深度域反射系數，ρ_i是第i層的密度，v_i是第i層的速度。

在步驟4中，在時間域，合成記錄是子波與反射系數的褶積：

$f\left(t\right)=w\left(t\right)*R\left(t\right)=\underset{0}{\overset{T}{\∫}}w\left(\mathrm{\τ}\right)R(t-\mathrm{\τ})d\mathrm{\τ}$

其中，w(t)和R(t)分別是時間域子波和反射系數，T是時間域子波周期，現在，將時間域子波w(t)轉換成深度域子波w(h)，深度域子波周期H(v)由步驟2計算得到，由速度和密度曲線得出深度域反射系數R(h)，用τ代表時間延遲，基于深變子波的合成記錄公式如下：

本發明以子波、速度、密度為輸入，建立子波與速度的準確的函數關系，即深變子波，進而正確計算子波在每一時刻的長度；當欠缺密度曲線時，可以根據陸相沉積環境當中不同沉積相態，給定針對性的擬合公式，計算出更真實的密度曲線，有利于反射系數的準確合理計算，然后，將深度子波與反射系數進行褶積，得到深度域的合成記錄結果。該裝置解決了深度域子波長度隨速度變化的難題，并且可以根據具體的沉積相態得到更合理的密度曲線，從而大大提高了深度域合成記錄制作的準確率。

附圖說明：

圖1為基于深變子波的合成記錄制作裝置示意圖；

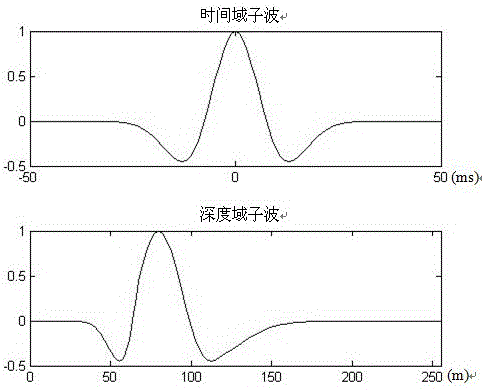
圖2為時間域子波轉換成深度域子波示意圖；

圖3為不同參數的Gardner公式擬合密度曲線對比圖；

圖4為時間域和深度域合成記錄結果對比圖。

具體實施方式：

為使本發明的上述和其他目的、特征和優點能更明顯易懂，下文特舉出較佳實施例，并配合附圖所示，作詳細說明如下。

如圖1所示，圖1為本發明的基于深變子波的合成記錄制作方法的流程圖。

在步驟101中，收集時間域子波、速度曲線和密度曲線，并且進行輸入。如果沒有密度曲線，可以在后面的步驟104中生成。

在步驟102中，通過建立時間域子波與速度的函數關系，將時間域子波轉換成深度域子波，即生成深變子波。

設定w(t)是時間域雷克子波，w(h)是深度域子波，v是速度曲線，計算深度為h時，深度域子波w(h)的形態。

假設，t時刻的時間域子波w(t)與深度h的深度域子波w(h)相對應，t^/時刻的時間域子波w(t^/)相對應的深度域子波是w(h^/)。

若將t與t^/之間的時間平均分成n份，那么時間間隔Δt＝(t^/-t)/n。

假設，時刻t₁＝t-Δt，t₂＝t-2Δt，與t₁時刻對應的深度是h₁，與t₂時刻對應的深度是h₂，那么

如公式1和公式2所述，對于時間域子波w(t)周期T內的任意時刻t^/都可以很方便地計算出所對應的深度值h^/，從而找準任意時刻的w(t^/)所對應的深度域子波w(h^/)，并且由公式3可以計算出由于速度變化而時刻改變的深度域子波周期H(v)。

將時間域子波轉換到深度域后，由于速度的影響，波形隨深度發生壓縮或拉伸兩種變化，如附圖2所示。圖2中，時間域子波是零相位雷克子波，通過本發明將其轉換成圖2中的深度域子波，可以看出，雷克子波在時間域是“時不變”子波，轉換到深度域后為“深變”子波，由于速度的影響，波形隨深度發生壓縮或拉伸兩種變化。

在步驟103中，判斷步驟101是否輸入密度曲線，如果沒有密度曲線，則進入到步驟104；如果有密度曲線，則進入到步驟105。

在步驟104中，根據陸相沉積環境當中不同沉積相態，給定針對性的擬合公式，計算密度曲線。

當只有速度曲線，欠缺密度曲線時，必須首先根據實際工區資料，擬合出比較符合實際的密度曲線。Gardner在1974年給出的密度與速度的經驗公式是

D＝αv_p^β (公式4)

其中D是密度，v_p是縱波速度，α＝0.31，β＝0.25。該公式直到今天仍被廣泛使用，但是它并不是放之四海皆準的公式，本專利會根據實際工區，針對α、β做出相應的調整。當α、β取不同的參數值時，計算出的密度曲線存在差異，如附圖3所示。該圖中，(a)是速度曲線；(b)是α＝0.31，β＝0.25時，計算的密度曲線；(c)是α＝0.25，β＝0.27時，計算的密度曲線。可以看出，當α、β取不同值時，計算出來的密度曲線存在差異，需要根據實際工區的情況，對α、β這兩個參數進行調整。

在步驟105中，根據實際工區資料，使用速度和密度曲線，得到準確的反射系數。

當有真實的速度曲線和密度曲線時，由如下公式可以得到每一深度的的反射系數：

其中R_i是第i層與第i+1層界面的深度域反射系數，ρ_i是第i層的密度，v_i是第i層的速度。

在步驟106中，將深變子波與反射系數進行褶積，制作深度域合成記錄。

在時間域，合成記錄是子波與反射系數的褶積：

$f\left(t\right)=w\left(t\right)*R\left(t\right)=\underset{0}{\overset{T}{\∫}}w\left(\mathrm{\τ}\right)R(t-\mathrm{\τ})d\mathrm{\τ}$

其中，w(t)和R(t)分別是時間域子波和反射系數，T是時間域子波周期。現在，將時間域子波w(t)轉換成深度域子波w(h)，深度域子波周期H(v)由步驟2計算得到，由速度和密度曲線得出深度域反射系數R(h)，用τ代表時間延遲。基于深變子波的合成記錄公式如下：

因為基于深變子波的合成記錄考慮了地層速度的影響，所以能準確刻劃出地層界面的真實深度，并且由于受到地層速度的影響，深度域合成記錄反射軸的胖瘦與時間域不同，如附圖4所示。該圖中，上圖是時間域合成記錄結果，下圖是深度域合成記錄結果。從兩種合成記錄結果的對比來看，深度域合成記錄結果能刻劃出地層界面的真實深度，并且由于受到地層速度的影響，深度域合成記錄反射軸的胖瘦與時間域不同。

該基于深變子波的合成記錄制作方法解決了深度域子波長度隨速度變化的難題，并且可以根據具體的沉積相態得到更合理的密度曲線，從而大大提高了深度域合成記錄制作的準確率。