本發明屬于電力系統直流輸電領域，特別涉及一種同塔雙回直流輸電線路的暫態行波時域計算方法。

背景技術：

在輸電走廊資源日益緊張的情況下，兩回直流輸電系統采用相同的輸電走廊，即同塔雙回直流線路，得到了具體的工程應用。直流輸電線路作為直流系統的重要組成部分，由于送電距離長，工作環境復雜，是直流系統中故障率最高的元件。準確、快速地直流線路故障識別以及故障定位，能有效減輕直流線路故障所造成的影響，加快故障恢復時間，從而確保交直流系統的安全穩定運行。目前，在實際工程中包括同塔雙回直流線路在內各類直流線路的主保護及其故障測距均采用行波原理，因此，直流線路故障后的暫態行波計算對直流輸電線路的穩定運行起到重要作用。

現有的行波暫態計算方法往往是基于固定參數的分布參數模型、無畸變線路模型或貝杰龍線路模型，無法計及線路的頻變特性，這對于分析直流線路故障所產生的寬頻暫態電氣量，將會產生較大誤差。另一方面，針對直流線路極線間的電磁耦合問題，由于單回直流線路為平衡線路，因此通過簡單的相模變換即可將其解耦而獨立進行分析。然而同塔雙回直流線路與單回直流線路相比，極線數目增加，必然帶來的故障類型的增多，如不同回直流極線的跨線故障，極線間的電磁耦合特性也更加復雜；而更值得注意的是，同塔雙回直流線路為不對稱線路，進行相模變換時線路的解耦矩陣將由固定的常數矩陣變為頻變矩陣。現有的直流線路行波暫態計算方法更是無法考慮這一因素的影響。

隨著越來越多的直流工程投入運行，直流輸電的復雜程度增加，對直流線路暫態行波計算的精度要求也越來越高。針對上述情況，從行波計算原理、策略上加以創新與改進，提高行波計算精度有著重要的理論和工程價值。

技術實現要素：

本發明的目的在于克服現有技術的缺點與不足，提供一種同塔雙回直流輸電線路的暫態行波時域計算方法，本發明考慮了線路頻變參數和同塔雙回線路的電磁耦合與不對稱性的影響因素，極大地增加了線路行波計算的精確性，提高了直流輸電線路保護和測距的精度。

本發明通過以下技術方案實現：一種同塔雙回直流輸電線路的暫態行波時域計算方法，包括以下步驟：

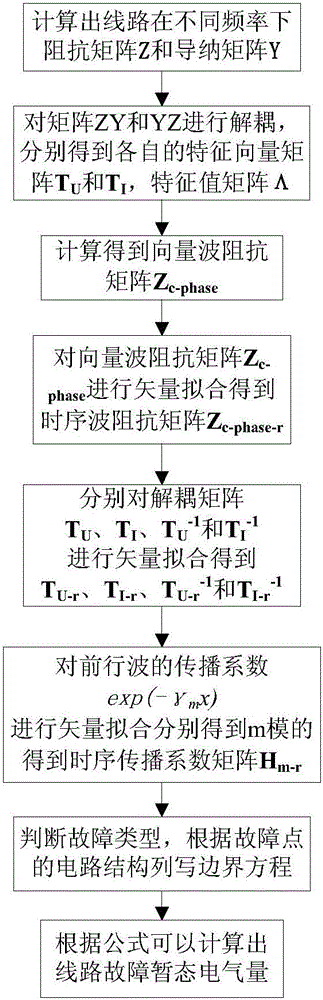
S1、計算出線路在不同頻率下的串聯阻抗矩陣Z和并聯導納矩陣Y；

S2、對矩陣ZY和YZ進行解耦，分別得到各自的特征向量矩陣T_U和T_I，以及特征值矩陣Λ；

S3、根據并聯導納矩陣Y、特征向量矩陣T_I和特征值矩陣Λ計算得到向量波阻抗矩陣Z_c-phase；

S4、對向量波阻抗矩陣Z_c-phase進行矢量擬合并進一步計算得到時序波阻抗矩陣Z_c-phase-r；

S5、分別對矩陣T_U、T_I、T_U^-1和T_I^-1進行矢量擬合得到T_U-r、T_I-r、T_U-r^-1和T_I-r^-1；

S6、分別對不同模量的前行波的傳播系數exp(-γ_mx)進行矢量擬合，得到對應的m模的時序傳播系數矩陣H_m-r，m＝0,1,2,3代表不同的模量；

S7、判斷故障類型，根據故障點的電路結構列寫邊界方程：

U_I-P、U_I-N、U_II-P、U_II-N為線路電壓，I_I-P、I_I-N、I_II-P、I_II-N為線路電流；

S8、根據上述方法計算出線路故障暫態電氣量；

優選的，步驟S1中，串聯阻抗矩陣Z的各元素為：

其中，Z_ii為導線i的自阻抗；Z_ik為導線i和k之間的互阻抗；R_i為導線i的電阻；h_i為導線i對地面高度；h_k是導線k對地面的高度；r_gm為導線的幾何均距；x_ik為導線i和k的水平距離；為復數深度；j為虛數單位，μ₀為真空磁導率，μ₀＝4π×10^-7H/m,，ω表示角頻率；

線路并聯導納矩陣Y：

Y＝G+jω·P^-1

其中，G為線路電導矩陣，其值遠遠小于電納，可以忽略不計；電位系數矩陣P為：

ε₀表示真空介電常數，ε₀＝8.854187817×10^-12F/m。

優選的，步驟S3中向量波阻抗矩陣Z_c-phase的計算公式：

優選的，步驟S4的具體步驟如下：

將向量波阻抗矩陣Z_c-phase中的每一個元素進行拉普拉斯變換再對其擬合，如下：

其中，TN為擬合階數；s為拉普拉斯算子，c_N、a_N、d和e均為由擬合確定的常數；

當前行電流為階躍信號時，(Z_c-phase)_ij對應產生的時域電壓為：

U_sI-ij(t)＝L^-1(Z_c-phase-ij(s)/s)

(Z_c-phase)_ij指的是向量波阻抗矩陣內的元素，L^-1表示拉普拉斯逆變換，將頻域電壓轉換為時域電壓；

由于線路的衰變作用，在直流線路傳播的行波信號實際上都不是階躍信號。但根據疊加定理，在t＝0時刻注入的任一電流i(t)均可視為階躍電流ε(t)的疊加：

因此可以將U_sI-ij(t)應用于上式中的每一個階躍信號，即將上式中的ε(t)均替換為U_sI-ij(t)，所以注入的電流i(t)產生的響應電壓U_ij(t)為：

考慮到實際裝置測量的均為離散信號，且當t<0時，U_sI-ij(t)＝0，因此上式可以化簡為如下形式：

其中，Δt為采樣時間間隔；k_m為：

k_m＝U_sI-ij(m·Δt)-U_sI-ij((m-1)Δt)

不妨將上式在nΔt時間內，寫成矩陣形式：

U_ij＝Z_iji

其中：U_ij＝[U_ij(0)U_ij(Δt)…U_ij(nΔt)]^T，為U_ij(t)按時間排列的列矩陣；i＝[i(0)i(Δt)…i(nΔt)]^T，為i(t)按時間排列的列矩陣；Z_ij設為(Z_c-phase)_ij的時域響應矩陣：

由于U_sI-ij(t)可計算獲得，因此對于已知線路，Z_ij可認為是常數矩陣；因而，當僅存在前行波時，電壓相量方程可寫成如下形式：

式中，電壓、電流矩陣均為對應函數按時間排列的列矩陣；Z_c-phase-r為由Z_ij組成的矩陣，其描述了同塔雙回直流線路行波電壓、電流之間的時域關系，定義為時序波阻抗矩陣。

進一步的，步驟S5中，所述的解耦矩陣T_U、T_I、T_U^-1和T_I^-1的矢量擬合皆與步驟S4中向量波阻抗矩陣的擬合過程相似，以T_U^-1為例：

i表示對T求逆，即iT_u-r＝T_U-r^-1；

同塔雙回直流輸電線路的向量和模量電壓滿足以下時域關系：

式中[U_4-0U_4-1U_4-2U_4-3]^T表示模量電壓。

進一步的，步驟S6中，γ_m為m模量的傳播系數，等于ZY和YZ特征值的平方根；由于行波傳播需要時間，因此exp(-γ_mx)會導致行波信息產生時移，因此對exp(-γ_mx)進行擬合前，exp(-γ_mx)需要乘以延時系數exp(τs)，其中τ表示時延，s為拉普拉斯算子，τs可提前計算，等于傳播距離與波速的比值；對exp(-γ_mx)進行擬合：

式中：Δx為單位傳播距離；擬合后，可根據疊加定理，求取exp(-γ_mΔx)的時域響應矩陣H_m-r，其處理過程依舊與步驟S4近似；以3模分量為例，3模分量的傳播系數矩陣的擬合計算結果如下：

因此不考慮反行波時，其時域表現形式為：

U_Fm-Δx＝H_m-rU_Fm-0

其中，U_Fm-x為m模在x點處的前行波電壓按時間排列的列矩陣；H_m-r定義為時序傳播系數矩陣，U_Fm-0表示m模在線路x＝0處的前行波電壓按時間排列的列矩陣；根據上式，在x＝LΔx處，L為單位傳播距離的個數，電壓列矩陣為：

U_Fm-LΔx表示任意距離的前行電壓波按時間排列的列向量。

本發明與現有技術相比，具有如下優點和有益效果：

1、考慮了線路參數頻變的影響，解決了同塔雙回直流線路不平衡所帶來的線路解耦問題。

2、所提出的方法僅在時域中進行計算，避免了復雜的時頻域轉換過程，為應用于保護控制研究提供了可能。因此本發明可大大提高直流線路行波的計算精度，而且有效的考慮了行波傳播過程中的色散現象和電磁暫態耦合，驗證了所提出的行波計算方法的計算精度和工程適用性。

附圖說明

圖1為實施例中計算方法的流程圖；

圖2為同塔雙回直流極線排布圖；

圖3為同塔雙回線路故障點的故障分量電路圖；

圖4為距離故障點627km處暫態電壓仿真值與計算值比較圖；

圖5為距離故障點627km處暫態電流仿真值與計算值比較圖；

圖6為距離故障點627km處暫態電壓變化量仿真值與計算值比較圖。

具體實施方式

下面結合實施例及附圖對本發明作進一步詳細的描述，但本發明的實施方式不限于此。

本發明的原理如下：

根據均勻傳輸線模型，同塔雙回直流線路電壓電流滿足如下關系：

四根極線用1P、1N、2P、2N表示，1P、1N分別表示第1回線的正極線、負極線，2P、2N分別表示第2回線的正極線和負極線。

其中，U_phase＝[U_I-P U_I-N U_II-P U_II-N]^T為線路電壓列向量；I_phase＝[I_I-P I_I-N I_II-PI_II-N]^T為線路電流列向量；Z、Y分別為輸電線路的串聯阻抗矩陣和并聯導納矩陣，與線路參數相關，為頻率的函數矩陣。同塔雙回直流線路呈現梯形排布，如圖1所示，因此Z和Y的非對角線元素不全部相等。

由(1)式推導可得：

其中ZY和YZ存在以下關系：

(3)式中Λ為ZY和YZ的特征值矩陣，而T_U和T_I分別為ZY和YZ的特征向量矩陣，T_U＝(T_I’)^-1，因此，(2)式又可以寫成如下形式：

此式中，U_mode＝T_U^-1U_phase＝[U₀ U₁ U₂ U₃]^T，為解耦得到的0、1、2和3模量電壓列向量；I_mode＝T_I^-1I_phase＝[I₀ I₁ I₂ I₃]^T，為模量電流列向量；T_U和T_I為電壓和電流的解耦矩陣。

當線路為平衡線路或者對稱換位時，ZY＝YZ，可得T_U＝(T_I’)^-1＝T_I，電壓電流的解耦矩陣相同且為固定的常數矩陣，如單回直流線路的解耦矩陣。

但當線路不換位時，如同塔雙回直流線路，T_U≠T_I且隨頻率而變化。

由(4)式可得到電壓電流的通解為：

其中：x為傳播距離；γ_m為m模量的傳播系數，等于ZY和YZ特征值的平方根；下標Fm和Bm分別代表m模的前行波和反行波。根據上式可以發現雖然同塔雙回直流線路的電壓、電流解耦矩陣不同，但是其傳播系數exp(γ_mx)和exp(-γ_mx)相同。

將T_U、T_I以及公式(5)代入公式(1)，僅考慮前行波時，可得到：

U_mode＝Z_c-modeI_mode (6)

當僅考慮反行波時，可得到：

U_mode＝-Z_c-modeI_mode (7)

式中：Z_c-mode＝(T_U)^-1Y^-1T_I(Λ)^0.5為模量波阻抗矩陣，體現了模量電壓和電流之間的頻域關系。當輸電線路為平衡線路時，Z_c-mode為對角矩陣，其中對角元素為對應模量的波阻抗。但當線路非對稱時，Z_c-mode的非對角線元素不全為0。

若將T_U和T_I代入上式，可得：

U_phase＝Z_c-phaseI_phase (8)

其中：Z_c-phase＝Y^-1T_I(Λ)^0.5(T_I)^-1為向量波阻抗矩陣，體現了極線電壓和電流之間的頻域關系。

可以發現：同塔雙回直流線路的電壓和電流解耦矩陣不同；其解耦矩陣和波阻抗等均為頻域參數，且受到線路參數頻變的影響，不為固定常數；解耦后的模量電壓(電流)行波間相互獨立。

本發明方法通過矢量擬合和疊加定理，將向量波阻抗矩陣，解耦矩陣和傳播系數等效成由線路參數決定的常數矩陣。

本實施例提出一種基于上述原理的同塔雙回直流輸電線路的暫態行波時域計算的實現方法，包括以下步驟：

S1.計算線路在不同頻率下的串聯阻抗矩陣Z和并聯導納矩陣Y：

串聯阻抗矩陣Z的各元素為：

其中，Z_ii為導線i的自阻抗；Z_ik為導線i和k之間的互阻抗；R_i為導線i的電阻；h_i為導線i對地面高度；h_k是導線k對地面的高度；r_gm為導線的幾何均距；x_ik為導線i和k的水平距離；為復數深度；j為虛數單位，μ₀為真空磁導率，μ₀＝4π×10^-7H/m,，ω表示角頻率。

線路并聯導納矩陣Y：

Y＝G+jω·P^-1 (10)

其中，G為線路電導矩陣，其值遠遠小于電納，可以忽略不計；電位系數矩陣P為：

ε₀表示真空介電常數，ε₀＝8.854187817×10^-12F/m。

S2.對矩陣ZY和YZ進行解耦，分別得到各自的特征向量矩陣T_U和T_I，特征值矩陣Λ；

S3.通過公式計算得到向量波阻抗矩陣Z_c-phase；

S4.對向量波阻抗矩陣Z_c-phase進行矢量擬合得到時序波阻抗矩陣Z_c-phase-r；

矢量擬合的具體步驟如下：

將向量波阻抗矩陣Z_c-phase中的每一個元素進行拉普拉斯變換并且再對其擬合，如下：

其中，TN為擬合階數；s是指拉普拉斯的算子，c_N、a_N、d和e均為由擬合確定的常數。

當前行電流為階躍信號時，(Z_c-phase)_ij對應產生的時域電壓為：

U_sI-ij(t)＝L^-1(Z_c-phase-ij(s)/s) (13)

(Z_c-phase)_ij指的是向量波阻抗矩陣內的元素，L-1是拉普拉斯逆變換，將頻域電壓轉換為時域電壓。

由于線路的衰變作用，在直流線路傳播的行波信號實際上都不是階躍信號。但根據疊加定理，在t＝0時刻注入的任一電流i(t)均可視為階躍電流ε(t)的疊加：

因此可以將U_sI-ij(t)應用于上式中的每一個階躍信號，即將(14)式中的ε(t)均替換為U_sI-ij(t)，所以注入的電流i(t)產生的響應電壓U_ij(t)為：

考慮到實際裝置測量的均為離散信號，且當t<0時，U_sI-ij(t)＝0，因此(15)式可以化簡為如下形式：

其中，Δt為采樣時間間隔；k_m為：

k_m＝U_sI-ij(m·Δt)-U_sI-ij((m-1)Δt) (17)

不妨將上式在nΔt時間內，寫成矩陣形式：

U_ij＝Z_iji (18)

其中：U_ij＝[U_ij(0)U_ij(Δt)…U_ij(nΔt)]^T，為U_ij(t)按時間排列的列矩陣；i＝[i(0)i(Δt)…i(nΔt)]^T，為i(t)按時間排列的列矩陣；Z_ij設為(Z_c-phase)_ij的時域響應矩陣：

由于U_sI-ij(t)可通過式(13)計算獲得，因此對于已知線路，Z_ij可認為是常數矩陣。因而，當僅存在前行波時，電壓相量方程可寫成如下形式：

式中，電壓、電流矩陣均為對應函數按時間排列的列矩陣。Z_c-phase-r為由Z_ij組成的矩陣，其描述了同塔雙回直流線路行波電壓、電流之間的時域關系，定義為時序波阻抗矩陣。

S5.分別對矩陣T_U、T_I、T_U^-1和T_I^-1進行矢量擬合得到T_U-r、T_I-r、T_U-r^-1和T_I-r^-1，其擬合過程與向量波阻抗相似，以T_U^-1為例：

i表示對T求逆，即iT_u-r＝T_U-r^-1；

同塔雙回直流輸電線路的向量和模量電壓滿足以下時域關系：

式中[U_4-0 U_4-1 U_4-2 U_4-3]^T表示模量電壓。

S6.分別對不同模量的前行波的傳播系數exp(-γ_mx)進行矢量擬合，得到對應的m模的時序傳播系數矩陣H_m-r，m＝0,1,2,3代表不同的模量；

γ_m為m模量的傳播系數，等于ZY和YZ特征值的平方根；由于行波傳播需要時間，因此exp(-γ_mx)會導致行波信息產生時移，因此對exp(-γ_mx)進行擬合前，exp(-γ_mx)需要乘以延時系數exp(τs)，其中τ表示時延，s為拉普拉斯算子，τs可提前計算，等于傳播距離與波速的比值。對exp(-γ_mx)進行擬合：

式中：Δx為單位傳播距離。擬合后，可根據疊加定理，求取exp(-γ_mΔx)的時域響應矩陣H_m-r，其處理過程依舊與Z_ij近似。以3模分量為例，3模分量的傳播系數矩陣的擬合計算結果如下：

因此不考慮反行波時，其時域表現形式為：

U_Fm-Δx＝H_m-rU_Fm-0 (27)

其中，U_Fm-x為m模在x點處的前行波電壓按時間排列的列矩陣；H_m-r定義為時序傳播系數矩陣，U_Fm-0表示m模在線路x＝0處的前行波電壓按時間排列的列矩陣。根據上式，在x＝LΔx處(上述公式是基于單位傳播距離Δx，距離時固定的，但是實際工程，故障位置是線路上任意一點，L為單位傳播距離的個數)的電壓列矩陣為：

U_Fm-LΔx表示任意距離的前行電壓波按時間排列的列向量。

S7.判斷故障類型，根據故障點的電路結構列寫邊界方程：

S8.根據公式(23)(28)(29)可以計算出線路故障暫態電氣量：

具體的，不考慮行波折反射的影響，首先以I-P線路發生故障為例，圖3給出了同塔雙回線路故障點的故障分量電路圖，R＝10Ω，U_f＝-500kV。基于EMTDC/PSCAD的±500kV溪洛渡同塔雙回直流輸電線路模型，對所提出的行波暫態計算方法進行驗證，計算頻率10kHz。計算方法如下：

根據故障點的電路結構可以列寫邊界方程：

其中，U_a為線路I-P對地電壓，U_f為階躍電壓行波，電壓、電流矩陣為按時間排列的列矩陣。根據公式(31)，故障點處的故障分量電壓為：

經過傳播后，線路故障暫態電氣量為：

圖4和圖5分別給出了在距離故障點627km處的，不同極線的故障分量電壓和電流曲線。其中，實線為根據公式(33)的計算結果，虛線為基于頻變線路模型(Frequency Dependent Phase Model)的仿真結果，點劃線為基于貝杰龍模型(Bergeron Model)的計算結果。

由于解耦后的四個模量波速存在差異，其中三個模量波速接近光速，另一個模量波速較慢，因此在行波傳播中存在2個明顯波頭，分別出現在圖4和圖5中的約2ms和3.2ms。第一個波頭受線路頻變特性導致的色散影響較小，近似于階躍波，但由于貝杰龍模型并未考慮線路解耦的頻變特性，因此，貝杰龍模型的計算結果(點劃線)與本發明所提出方法的結果(實線)存在差異。而在受色散影響較大的第二個波頭到達后，計算誤差進一步增大。因此，沒有計及線路參數的頻變特性和線路參數排布不對稱的影響，是導致計算存在誤差的主要原因。

從圖4和圖5中的本發明所提出方法的結果(實線)和仿真結果(虛線)的對比可以發現，兩者基本重合，說明所提出同塔雙回行波時域計算方法可以有效的計及線路參數頻變和線路不對稱的影響，計算精度較高。

為了進一步對所提計算方法進行測試，圖6給出了I-P和I-N跨線接地故障情況下，I-P和II-N極線的暫態電壓變化量的計算結果(實線)和仿真結果(頻變線路模型，虛線)，分別代表故障極和健全極。根據圖6可發現，計算和仿真結果依然重合，證明了所提出行波計算方法對于不同類型的同塔雙回直流線路故障的適用性。

通過PSCAD/EMTDC的仿真發現本發明所提出的傳播計算方法的計算結果和依頻電線電路模型(Frequency Dependent Phase Model)仿真結果一致，能夠根在有效的考慮線路傳播過程中的色散現象和電磁暫態耦合的情況下，精準地計算。因此本發明可大大提高同塔雙回直流輸電線路暫態行波計算的精確性，有很高的工程適用性。

上述實施例為本發明較佳的實施方式，但本發明的實施方式并不受上述實施例的限制，其他的任何未背離本發明的精神實質與原理下所作的改變、修飾、替代、組合、簡化，均應為等效的置換方式，都包含在本發明的保護范圍之內。