本發明涉及一種基于有限時間觀測器的多智能體系統故障診斷方法，屬于應用于多智能體系統技術領域。

背景技術：

近些年來，作為一種可以有效處理復雜系統的工具，多智能體技術已經引起了廣泛的關注并被應用于多個重要領域。但是多智能體系統自身特有的網絡鏈接、自由分布、信息共享等優點，也讓其更容易受到故障的影響。當多智能體系統中的某一個智能體出現故障的時候，故障可通過多智能體系統特有的網絡鏈接去影響其他智能體，從而使整個多智能體系統遭受嚴峻的考驗。因此，為了提升多智能體系統的穩定性和安全性，針對其的故障診斷技術也應該給予高度的重視。故障診斷可分為故障檢測、故障分離和故障估計。故障診斷通過對系統運行狀況進行監測來判斷是否有故障發生，同時確定故障發生的具體信息，例如時間、位置和大小等。

現有的基于觀測器的故障診斷主要依靠于觀測器的穩態性能，依靠于觀測器是否穩定，即當時間趨近無窮大時，觀測器估計值與系統狀態形成的誤差能否無限接近平衡點。但由于多智能體系統，諸如需編隊飛行的飛行控制系統，是一項高耗費高投入的技術，針對其的故障診斷必須要有準確性和快速性。這就對故障診斷的暫態性能和收斂性能都做出了要求。因此，可以引進有限時間技術，有限時間即預先給定了一個有限的時間區間。在這個時間內，控制系統的狀態將會在這個有限時間內收斂到穩定平衡點。

中國專利申請2016108243782提出了“領導-跟隨型多智能體系統的有限時間魯棒故障診斷設計方法”，基于有向圖通訊拓撲結構，得出拉普拉斯矩陣；再針對每個節點建立狀態方程和輸出方程，并將狀態向量與故障向量增廣為新的向量；根據構建的有向圖，構造基于有向圖的分布式誤差方程與全局誤差方程；最后基于有限時間魯棒控制，得到多智能體系統的故障診斷觀測器的增益矩陣。但該方法還存在以下不足：一是該方法雖然考慮了外界干擾的存在，但在設計過程中只借助魯棒控制的設計思想在一定程度上減少其對故障診斷結果的不利影響，而不能徹底消除，這或多或少地在設計層面上造成了診斷準確性的降低；二是該方法采用的多智能體系統故障診斷的方法是需要在每一個智能體中都建立相對應的觀測器，成本較高；三是該方法雖然可以在有限時間內進行故障診斷，但是該有限時間不能進行預先設定，在線實時故障診斷的快速性還需進一步提高。

技術實現要素：

本發明提出了一種基于有限時間觀測器的多智能體系統故障診斷方法，通過在某一個特定的智能體中建立有限時間未知輸入觀測器從而觀測與其相鄰智能體的故障的方法，實現了對多智能體系統的分布式故障診斷。本發明中所設計的分布式故障診斷設計方法，可在理論上抑制外界時變干擾對故障診斷的影響，并可在預先設定的有限時間內，對各鄰接智能體中任意一個智能體出現的故障或多個智能體同時出現故障時實行有效準確的有限時間在線診斷和故障估計。

本發明為解決其技術問題采用如下技術方案：

一種基于有限時間觀測器的多智能體系統故障診斷方法，包括如下具體步驟：

第一步：通過多智能體系統間的通訊鏈接，構建多智能體系統連接圖并以無向圖表示，從而得出加權鄰接矩陣λ；

第二步：針對每個智能體，通過在工作點進行局部線性化的方法，得到該多智能體系統的局部動態方程，并根據得到的無向圖建立多智能體系統的全局動態方程；

第三步：在多智能體系統中任意選取一個智能體，重構多智能體系統的全局動態方程，此時的系統輸出由與該智能體相關的局部動態信息構成；

第四步：通過兩個坐標變換，將第三步中得到的系統動態方程分解成三個子系統，并得到沒有包含未知輸入的降階子系統；

第五步：通過在選取的智能體中設計兩個獨立的觀測器，基于有限時間理論，構造出一個在預設時間內收斂的有限時間未知輸入觀測器；根據該有限時間觀測器得到的狀態估計值和一個故障診斷律在有限時間內完成對鄰接智能體的在線故障診斷和故障估計。

第一步中得出加權鄰接矩陣λ的具體方式為：

設由一組頂點和邊構成一個完整的多智能體系統的無向圖，其中v＝{v1,v2,...,vn}定義為頂點的集合，v1為第1個智能體，v2為第2個智能體，vn表示第n個智能體；ε＝{(vi,vj):vi,vj∈v}定義為邊的集合；頂點νi與vj分別表示第i個智能體和第j個智能體，i,j∈{1,2,...,n}且i≠j；邊(νi,νj)用來表示智能體j可以接收智能體i的信息；定義與頂點νp相鄰頂點的集合為np＝{vj∈v:(vp,vj)∈ε,p≠j}；

定義λ＝[aij]∈r^n×n表示該無向圖的加權鄰接矩陣，其中aij表示每條邊的權重；若(νi,νj)∈ε，則aij＝1，否則aij＝0；并且aii＝0。

第二步中所述多智能體系統的局部動態方程：

上述方程中，xi(t)和yi(t)分別是每個智能體的狀態向量和輸出向量，表示每個智能體狀態向量的微分項，ui(t)是各個智能體的控制輸入向量，fi(t)為系統故障，di(t)為外界時變擾動向量；a、b、c分別為所述多智能體系統的狀態矩陣、輸入矩陣、輸出矩陣，矩陣e是故障分布矩陣，矩陣d為擾動分布矩陣。

所述第三步中，任意選取一個智能體p，其中p∈(1～n)，基于無向圖，依據智能體p,該多智能體系統的全局動態方程重構為：

其中：fr(t)表示發生在第r(r∈np)個智能體中的故障，且f-r(t)表示從全局故障f(t)中移除fr(t)后的矩陣，是相應于fr(t)的分布矩陣，且為的一個子矩陣，而表示從中移除后余下的子矩陣，表示智能體p的局部動態信息，表示集合的基數，其中表示智能體p相鄰頂點的集合與智能體p組成的合集；表示局部信息矩陣且為列滿秩矩陣，其中in表示一個n×n維的單位陣，是一個行滿秩矩陣且為加權鄰接矩陣λ的一個子矩陣。

定義所述多智能體系統的全局動態方程：

(3)表示為：

第四步中所述將得到的系統動態方程分解成三個子系統的具體方法為：

假設矩陣與矩陣m都為列滿秩矩陣，鑒于也是列滿秩矩陣，定義rank(m)＝l，(l+q≤p)；其中，rank(x)表示一個矩陣x的秩；

假設在這種情況下，矩陣將會存在左偽逆：其中，表示一個矩陣x的左偽逆；

首先對系統的狀態方程進行坐標變換，定義一個非奇異矩陣：

其中：w＝p1w0，w∈r^nn×(nn-l-q)，w0是任意一個令矩陣非奇異的矩陣，方陣并滿足p1²＝p1，即p1是一個冪等矩陣，其中inn為一個nn×nn維的單位陣；

通過非奇異矩陣t，系統(4)被分解為：

其中：定義為系統分解后的狀態向量，為系統分解后的狀態向量的微分項，分別為所述多智能體系統分解后的狀態矩陣、輸入矩陣、輸出矩陣，矩陣是分解后的故障分布矩陣，矩陣為分解后的擾動分布矩陣，具體如下：

且有和均表示分解后的狀態向量；均為分解后的狀態矩陣；同樣地，和表示分解后的輸入矩陣，t為上述所求得的非奇異矩陣，t^-1為矩陣t的逆矩陣；il與iq分別表示一個l×l維的單位陣和一個q×q維的單位陣；

與的微分項都分別直接被fr(t)與ω(t)兩項未知輸入所影響，移除與的微分項后，系統(5)可寫為：

其中：inn-l-q為一個(nn-l-q)×(nn-l-q)維的單位陣，

接下來對系統的輸出方程進行坐標變換，定義一個非奇異矩陣：

其中：q＝p2q0，q∈r^p×(p-l-q)，q0選取為任意一個令矩陣非奇異的矩陣；方陣并滿足p2²＝p2，即p2是一個冪等矩陣；

定義u1(t)∈r^l×p，u2(t)∈r^q×p，u3(t)∈r^(p-l-q)×p，定義ip-l-q表示一個(p-l-q)×(p-l-q)維的單位陣，則有：

顯然，有和其中，0l×(nn-l-q)和0q×(nn-l-q)分別表示l×(nn-l-q)維和q×(nn-l-q)維的零矩陣；再對(6)中的輸出方程等式兩邊同時左乘u^-1得到：

通過這些等式，得到所需的降階子系統：

其中：為降階輸出分布矩陣，為降階輸出向量。

所述第五步中通過在選取的智能體中設計兩個獨立的觀測器，基于有限時間理論，構造出一個在預設時間內收斂的有限時間未知輸入觀測器的方法是：

首先，假設是能觀的，那么兩個獨立的觀測器設計為：

其中：z1(t)與z2(t)分別為構造的兩個觀測器的狀態向量，與分別為z1(t)與z2(t)的微分項，且l1與l2是需要設計的觀測器增益矩陣；

其次，通過定義：

其中：

上述兩個獨立的觀測器構成一個觀測器，再加入一個時滯τ用來估計狀態則建立在選取的智能體p中的有限時間未知輸入觀測器設計為：

其中：表示狀態向量的估計值，t0表示初始時間，z(t-τ)即對觀測器狀態加上一個時滯τ，k＝[inn-l-q0nn-l-q][se^fτs]^-1，且inn-l-q表示一個(nn-l-q)×(nn-l-q)維的單位陣；對于z(t)，t∈[t0-τ,t0]，假定其中，且設為任意一個有界的常值。

所述第五步中的故障診斷律的具體形式為：

其中：表示狀態向量的估計值。

本發明的有益效果如下：

一是本發明設計的分布式故障診斷方法，采取在某個智能體中建立觀測器去監測其周邊智能體的方式，不需要針對每一個智能體都建立觀測器，大大減少了所需的觀測器數量，從而降低了系統診斷的成本。

二是本發明基于未知輸入觀測器對多智能體系統進行故障診斷，在設計觀測器的過程中，將系統擾動等視為未知輸入進行系統分解，這樣可以有效地減少外加干擾對系統診斷的影響，從而使故障診斷結果更為可靠。

三是本發明不僅考慮了觀測器的穩態性能，更考慮了觀測器估計過程的穩態性能和收斂性能，最終可以做到在預先設定的有限時間內進行在線診斷和故障估計，提高了故障診斷的準確性和快速性。

附圖說明

圖1為本發明實施驗證的實例所建立的具有四個智能體節點的多智能體系統無向圖，其中：圖標1—4分別表示該多智能體系統中的智能體1、智能體2、智能體3和智能體4。

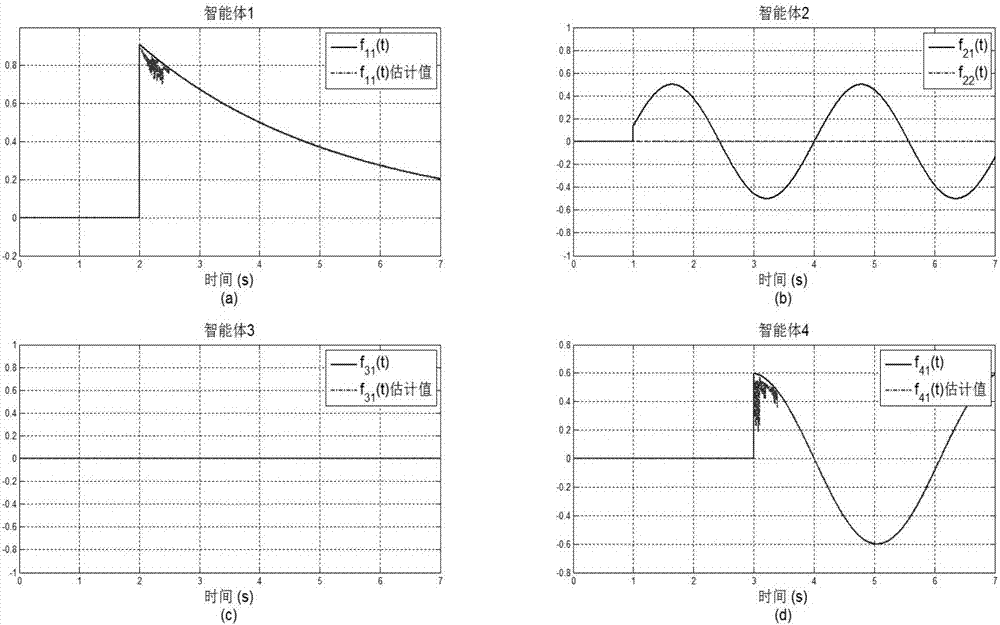
圖2為本發明實施例ι所測的智能體1、2、4同時出現故障時，通過本發明所設計的分布式故障診斷方法得到的結果示意圖；其中圖2(a)為智能體1的故障估計值與故障真實值的對比曲線示意圖；圖2(b)為智能體2中發生的故障真實值的示意圖；圖2(c)為智能體3的故障估計值與故障真實值的對比曲線示意圖；圖2(d)為智能體4的故障估計值與故障真實值的對比曲線示意圖。

圖3為本發明實施例ιι所測的智能體2、3、4同時出現故障時，通過本發明所設計的分布式故障診斷方法得到的結果示意圖。其中圖3(a)為智能體1的故障估計值與故障真實值的對比曲線示意圖；圖3(b)為智能體2中發生的故障真實值的示意圖；圖3(c)為智能體3的故障估計值與故障真實值的對比曲線示意圖；圖3(d)為智能體4的故障估計值與故障真實值的對比曲線示意圖。

具體實施方式

下面結合附圖對本發明創造做進一步詳細說明。

本發明以如下的某垂直起降飛機縱向運動方程為實施對象，針對其編隊飛行中出現的執行器故障，提出一種基于有限時間未知輸入觀測器的多智能體系統分布式故障診斷設計方法，該故障診斷方法可以提高故障診斷的暫態性能和收斂性能，使系統在預先設定的有限時間內完成在線診斷與故障估計；

考慮如下的某垂直起降飛機縱向運動方程：

其中，xi(t)和yi(t)分別是每個智能體的狀態向量和輸出向量，表示每個智能體狀態向量的微分項，ui(t)是各個智能體的控制輸入向量，fi(t)為系統故障，di(t)為外界時變擾動向量。a、b、c分別為所述多智能體系統的狀態矩陣、輸入矩陣、輸出矩陣，矩陣e是故障分布矩陣，矩陣d為擾動分布矩陣。系統各個矩陣表示如下：

假設該系統發生執行器故障：鑒于執行器故障是發生在控制輸入的部分，因此本發明有故障分布矩陣e＝b；假定系統的輸入擾動的分布矩陣是d＝[0010]^t。

首先，構建多智能體系統連接圖并以無向圖表示，得出加權鄰接矩陣λ：

設由若干個頂點和若干個邊組成一個完整的多智能體系統的無向圖，其中v＝{v1,v2,...,vn}定義為頂點的集合，v1為第1個智能體，v2為第2個智能體，vn表示第n個智能體；ε＝{(vi,vj):vi,vj∈v}定義為邊的集合；頂點νi與vj分別表示第i個智能體和第j個智能體，i,j∈{1,2,...,n}且i≠j；邊(νi,νj)用來表示智能體j可以接收智能體i的信息；定義與頂點νp相鄰頂點的集合為np＝{vj∈v:(vp,vj)∈ε,p≠j}。

定義λ＝[aij]∈r^n×n表示該無向圖的加權鄰接矩陣，其中aij表示每條邊的權重；若(νi,νj)∈ε，則aij＝1，否則aij＝0；并且aii＝0。

根據構建的無向圖，可以構造出該多智能體系統的全局動態方程：

其中：x(t)∈rⁿⁿ定義為該多智能體系統的全局狀態向量，表示全局狀態向量的微分項，y(t)為該多智能體系統的全局輸出向量，u(t)∈r^nm是全局控制輸入向量，為全局故障向量，為全局擾動向量，為全局狀態分布矩陣，為全局控制輸入分布矩陣，為全局擾動分布矩陣，為全局輸出分布矩陣，為全局故障分布矩陣。此外，in表示一個n×n維的單位陣，代表克羅內克積。具體如下：

其中：為第一個智能體的狀態向量的轉置，為第二個智能體的狀態向量的轉置，為第n個智能體的狀態向量的轉置；為第一個智能體的控制輸入向量的轉置，為第二個智能體的控制輸入向量的轉置，為第n個智能體的控制輸入向量的轉置；為第一個智能體的輸出向量的轉置，為第二個智能體的輸出向量的轉置，為第n個智能體的輸出向量的轉置；f1^t(t)為第一個智能體的故障向量的轉置，為第二個智能體的故障向量的轉置，為第n個智能體的故障向量的轉置；為第一個智能體的擾動向量的轉置，為第二個智能體的擾動向量的轉置，為第n個智能體的擾動向量的轉置。

進一步的，第二步所述的針對每個智能體的系統動態方程，其實現方法是對每個非線性系統在工作點進行線性化所得到。

進一步的，所述第三步中，任意選取一個智能體p(p∈(1～n))，基于無向圖，依據智能體p,該多智能體系統的全局動態方程可表示為：

其中：fr(t)表示發生在第r(r∈np)個智能體中的故障，且f-r(t)表示從全局故障f(t)中移除fr(t)后的矩陣。是相應于fr(t)的分布矩陣，且為的一個子矩陣，而表示從中移除后余下的子矩陣。表示智能體p可用的局部動態信息。表示集合的基數，其中表示智能體p相鄰頂點的集合與智能體p組成的合集。表示局部信息矩陣且為列滿秩矩陣，其中in表示一個n×n維的單位陣，是一個行滿秩矩陣且為加權鄰接矩陣λ的一個子矩陣。已知λ＝[aij]∈r^n×n，其中aij表示每條邊的權重，若(νi,νj)∈ε，則aij＝1，否則aij＝0。同理，λp中的元素表示上述集合中所包含的節點互相組成的每條邊的權重。

定義則(3)可以表示為：

進一步的，所述第四步中系統分解的具體方法為：

本發明中假設矩陣與矩陣m都為列滿秩矩陣，鑒于也是列滿秩矩陣，可以定義rank(m)＝l，(l+q≤p)。其中，rank(x)表示一個矩陣x的秩。

然后本發明中假設在這種情況下，矩陣將會存在左偽逆：其中，表示一個矩陣x的左偽逆。

首先對系統的狀態方程進行坐標變換，定義一個非奇異矩陣：

其中：w＝p1w0，w∈r^nn×(nn-l-q)，w0是任意一個可以令矩陣非奇異的矩陣。方陣并滿足p1²＝p1，即p1是一個冪等矩陣，其中inn為一個nn×nn維的單位陣。

通過非奇異矩陣t，系統(4)可以被分解為：

其中：定義為系統分解后的狀態向量，為系統分解后的狀態向量的微分項，分別為所述多智能體系統分解后的狀態矩陣、輸入矩陣、輸出矩陣，矩陣是分解后的故障分布矩陣，矩陣為分解后的擾動分布矩陣，具體如下：

且有和均表示分解后的狀態向量；均為分解后的狀態矩陣；同樣地，和表示分解后的輸入矩陣，t為上述所求得的非奇異矩陣，t^-1為矩陣t的逆矩陣。另外，il與iq分別表示一個l×l維的單位陣和一個q×q維的單位陣。

顯然，與的微分項都分別直接被fr(t)與ω(t)兩項未知輸入所影響，移除與的微分項后，系統(5)可寫為：

其中：inn-l-q為一個(nn-l-q)×(nn-l-q)維的單位陣，

接下來對系統的輸出方程進行坐標變換，定義一個非奇異矩陣：

其中：q＝p2q0，q∈r^p×(p-l-q)，q0可選取為任意一個令矩陣非奇異的矩陣。方陣并滿足p2²＝p2，即p2是一個冪等矩陣。

定義u1(t)∈r^l×p，u2(t)∈r^q×p，u3(t)∈r^(p-l-q)×p，定義ip-l-q表示一個(p-l-q)×(p-l-q)維的單位陣，則有：

顯然，有和其中，0l×(nn-l-q)和0q×(nn-l-q)分別表示l×(nn-l-q)維和q×(nn-l-q)維的零矩陣。再對(6)中的輸出方程等式兩邊同時左乘u^-1可以得到：

通過這些等式，可以得到所需的降階系統：

其中：為降階輸出分布矩陣，為降階輸出向量。

進一步的，所述第五步中設計有限時間未知輸入觀測器的方法是：

首先，本發明中假設是可觀的，那么兩個分離的觀測器可設計為：

其中：z1(t)與z2(t)分別為構造的兩個觀測器的狀態向量，與分別為z1(t)與z2(t)的微分項，且l1與l2是需要設計的觀測器增益矩陣。

其次，通過定義：

其中：

上述兩個獨立的觀測器可以構成一個觀測器，再加入一個時滯τ用來估計狀態則建立在選取的智能體p中的有限時間未知輸入觀測器可以設計為：

其中：表示狀態向量的估計值，t0表示初始時間，z(t-τ)即對觀測器狀態加上一個時滯τ，k＝[inn-l-q0nn-l-q][se^fτs]^-1，且inn-l-q表示一個(nn-l-q)×(nn-l-q)維的單位陣。由于設計的過程中包含時滯，那么觀測器必須要有一個初始條件。對于z(t)，t∈[t0-τ,t0]，不失一般性地，本發明中假定其中，且可設為任意一個有界的常值。

為了實現在有限時間內對多智能體系統的故障進行在線診斷與故障估計，本發明第五步所述的有限時間未知輸入觀測器必須滿足：

1)有界性：該觀測器的估計誤差在時間區間[t0,t0+τ]內必須保持有界；

2)收斂性：該觀測器可以在有限時間τ內收斂，即：

當該觀測器滿足以下兩個約束條件時：

1)f是穩定的；

2)det[s,e^fτs]≠0；

本發明第五步所述的有限時間未知輸入觀測器存在且可以保證估計過程中的有界性并在有限時間τ內估計出狀態其中，第二個約束條件det[s,e^fτs]≠0可以通過對觀測器增益l1與l2的選取來達到。給定任意一個標量σ＜0，當選取的l1與l2可以使

re(λi(f2))＜σ＜re(λj(f1))＜0，i,j＝1,...,nn-l-q

則對基本上任意一個τ∈r⁺，det[s,e^fτs]≠0都可以滿足，其中：λi(f2)表示矩陣f2的任意一個特征值，λj(f1)表示矩陣f1的任意一個特征值。

所述第五步中的故障診斷律的具體形式為：

其中：表示狀態向量的估計值，

為了防止不能在某些系統中得到，可以用來代替：

其中：α為大于零的標量，ypf(t)為代替輸出yp(t)構造的新的輸出向量，為ypf(t)的微分項。

這樣，故障診斷律變為：根據建立在智能體p中的有限時間觀測器得到的狀態估計值和該故障診斷律可以在有限時間內完成對其鄰接智能體r的在線故障診斷和故障估計。

如圖1所示，圖1中智能體1、智能體2、智能體3和智能體4代表該無向圖具有4個節點。從圖1中可以得出加權鄰接矩陣在本實施例中，選取智能體2建立有限時間未知輸入觀測器，用來對其周邊智能體進行故障診斷。由圖1可以看出，智能體2與其他三個智能體均相連，因此本實施例中則λp＝λ。具體實施過程中可以得到公式(3)中的兩項重要參數如下：

需要用到的兩個坐變換矩陣為：

應用matlab軟件，將預先設定的有限時間選取為τ＝1s，選取α＝0.001，將極點配置在[-2-1-2-2]和[-7-6-7-7]，可以得到：

為驗證本發明分布式故障診斷方法的效果，采用以下兩個仿真實施例來進行驗證，在兩例實施例中，均在系統模型中加入了噪聲作為擾動。

實施例ι

假設智能體1、2、4同時出現了故障：

第1個智能體出現的故障

第2個智能體出現的故障

第4個智能體出現的故障

圖2為本發明實施例ι所測的智能體1、2、4同時出現故障時，通過本發明所設計的分布式故障診斷方法得到的結果示意圖。其中圖2(a)為智能體1的故障估計值與故障真實值的對比曲線示意圖；圖2(b)為智能體2中發生的故障真實值的示意圖；圖2(c)為智能體3的故障估計值與故障真實值的對比曲線示意圖；圖2(d)為智能體4的故障估計值與故障真實值的對比曲線示意圖。且其中智能體2是本實施例中選為建立有限時間未知輸入觀測器的智能體，所以理論上在其中發生的故障不應該影響對其周邊智能體的故障診斷。

實施例ιι

假設智能體2、3、4同時出現故障，其中智能體2中出現的故障設定為與實施例ι中大小不變：

第3個智能體出現的故障

第4個智能體出現的故障

圖3為本發明實施例ιι所測的智能體2、3、4同時出現故障時，通過本發明所設計的分布式故障診斷方法得到的結果示意圖。其中圖3(a)為智能體1的故障估計值與故障真實值的對比曲線示意圖；圖3(b)為智能體2中發生的故障真實值的示意圖；圖3(c)為智能體3的故障估計值與故障真實值的對比曲線示意圖；圖3(d)為智能體4的故障估計值與故障真實值的對比曲線示意圖。且其中智能體2是本實施例中選為建立有限時間未知輸入觀測器的智能體，所以理論上在其中發生的故障不應該影響對其周邊智能體的故障診斷。

如附圖所示，當故障發生在智能體2周邊的智能體中時，建立在智能體2中的有限時間未知輸入觀測器可以在預先設定好的有限時間τ＝1s內完成在線診斷和故障估計。并且，發生在其他智能體中的故障，包括發生在智能體2中的故障都不會對故障診斷的結果產生影響。且由圖中曲線可以看出，本發明所用的未知輸入觀測器的方法，極大的抑制了外加噪聲的影響。

從仿真結果可以得出，當多智能體系統中一個或多個智能體出現故障時，只需要設計少量的觀測器，本發明設計的基于有限時間未知輸入觀測器分布式故障診斷方法即可以在預先設定的有限時間內進行在線診斷和故障估計，且可以良好地抑制外加時變干擾的影響。本發明對于多智能體系統在有限時間內的故障診斷與準確監測具有重要的實用參考價值。

本發明的具體實施方式中凡未涉到的說明屬于本領域的公知技術，可參考公知技術加以實施。

以上所述僅是本發明的優選實施方式，應當指出，對于本技術領域的普通技術人員來說，在不脫離本發明原理的前提下，還可以做出若干改進和潤飾，這些改進和潤飾也應視為本發明的保護范圍。