本發明涉及航空航天領域，具體地，涉及一種自適應的月球軟著陸軌道快速優化控制器。

背景技術：

在進行無人月面勘探或載人登月任務時，都需要使著陸器實現月球表面軟著陸，以保證儀器設備以及航天員的安全。在典型的月球軟著陸過程中，從環月軌道下降到月球表面主要可分為2個階段：霍曼轉移段和動力下降段。其中，霍曼轉移段指著陸器從環月停泊軌道通過霍曼變軌進入環月橢圓軌道，并運行至近月點；動力下降段指著陸器從近月點處開始發動機制動抵消水平速度，并最終以較小速度著陸月面。由于霍曼變軌速度增量較小，著陸器的大部分燃料都消耗在動力下降段，故有必要對動力下降段的著陸軌跡進行優化設計以減少燃料消耗。

將常推力月球軟著陸軌道離散化是求解月球軟著陸軌道問題的一種方法，而離散點處的狀態是求解的關鍵，可使用優化算法求解離散點的狀態。但是不恰當的優化算法導致規劃出非最優軌道，浪費大量的燃料。

技術實現要素：

為了減少月球軟著陸時消耗的燃料，本發明的目的在于提供一種自適應的月球軟著陸軌道快速優化控制器。

本發明解決其技術問題所采用的技術方案是：一種自適應的月球軟著陸軌道快速優化控制器，該軌道快速優化控制器由優化模塊、仿真模塊、執行模塊組成；其中：

仿真模塊把月球軟著陸軌道分割成n個小段，并將n的值輸入優化模塊；每個節點的時刻由式(1)得到：

其中，tk為第k+1個節點的時刻，k＝0,1,...,n，t0為初始時間，記t0＝0；

優化模塊把包括初始節點和終節點在內的n+1個節點的推力方向角ψ與軟著陸終端時刻tf作為待優化的參數；初始化種群規模為ns的粒子群，隨機生成維度為n+2的粒子i的初始位置xi＝(xi1,xi2,...,xi(n+2))和初始速度vi＝(vi1,vi2,...,vi(n+2))，i＝1,2,...,ns，并將粒子的位置信息傳入仿真模塊；定義維度變量d，d＝1,2,...,n+2；當d＝1,2,...,n+1時，xid代表第d個節點的推力方向角，當d＝n+2時，xid代表軟著陸終端時刻，xid∈[500,700]，vid∈[-200,200]；種群規模ns＝300～600；然后按以下方法進行迭代，初始時迭代計數t＝0：

(1)仿真模塊中，月球軟著陸過程中推力方向角表示成多項式(2)：

ψ(t)＝λ0+λ1t+λ2t²+λ3t³(2)

其中ψ(t)表示著陸軌道t時刻的推力方向角，λ0,λ1,λ2,λ3為系數；優化模塊輸入的粒子的位置代表n+1個節點的推力方向角及軟著陸終端時刻，按照式(1)得到n+1個節點的對應時刻；采用函數逼近法，利用n+1個節點的推力方向角及其對應時刻，對式(2)進行擬合，可以求得多項式的系數λ0,λ1,λ2,λ3，進而得到整個著陸軌道各個時刻的推力方向角ψ(t)；

(2)仿真模塊存儲了月球軟著陸時著陸器的質心動力學方程，見式(3)：

式(3)中r為著陸器的月心距離，v為著陸器的徑向速度，θ為著陸器極角，ω為著陸器極角角速度，μ為月球引力常數，m為著陸器質量，f為制動發動機推力，isp為制動發動機比沖；其中月球引力常數μ為常數，μ＝4902.75km³/s²，制動發動機推力f與制動發動機比沖isp與實際使用的發動機有關，也為常數；著陸器初始質量m0根據實際確定；其他參數在著陸器著陸過程中發生變化；

初始條件為：

其中，rp和ra分別為霍曼轉移段的近地點半徑和遠地點半徑，rp＝1753km，ra＝1838km；

將步驟(1)中擬合得到的推力方向角ψ(t)、式(4)的初始條件以及著陸器初始質量m0帶入動力學方程(3)，所有數據單位統一，獲得月球軟著陸的軌道，并將獲得的軌道信息輸入給優化模塊；

(3)優化模塊中，優化目標為軟著陸過程消耗燃料最少，即令式(5)中指標j最大：

同時，為實現軟著陸，終端約束條件為：

其中，r為月球半徑，r＝1738km；

在適應度函數中考慮約束條件，構造適應度函數fitness：

fitness＝j-α[(r(tf)-r)²+v²(tf)+ω²(tf)](7)

其中r(tf)、v(tf)、ω(tf)分別表示仿真模塊輸入的軟著陸軌道終端時刻的月心距離、徑向速度、極角角速度；α為罰因子，α＝10000；根據仿真模塊輸入的軟著陸軌道，按照式(7)計算適應度函數值；適應度函數值最大的粒子為全局最優粒子，其位置為pbest＝(pbest1,pbest2,...,pbest(n+2))；

(4)在優化模塊中對所有粒子進行分群操作，包括以下子步驟：

(4.1)將所有粒子按照適應度函數值大小從大到小排序，選取適應度函數值最大的粒子作為一個子群中心；

(4.2)在剩下的粒子中選取適應度函數值最大的粒子，依次計算該粒子與各個子群中心的歐幾里得距離；粒子i與粒子j的歐幾里得距離dist(i,j)定義為：

其中，xi＝(xi1,xi2,...,xi(n+2))代表粒子i的位置，xj＝(xj1,xj2,...,xj(n+2))代表粒子j的位置，i,j＝1,2,...,ns；若該粒子與某一個子群中心的歐幾里得距離小于半徑r，則將該粒子歸為該子群中心所在的子群，并不再計算該粒子與剩下的子群中心的歐幾里得距離；若該粒子與所有子群中心的距離都大于半徑r，則將該粒子置為一個新的子群中心；半徑r＝15～25；

(4.3)重復步驟4.2)，直到處理完所有粒子，則分群完成，且每個子群中心為該子群中適應度函數值最大的粒子；

(5)檢查每個子群中的粒子數，若一個子群中的粒子數為s，且s>smax，smax為子群允許的最大粒子數，則將適應度最差的(s-smax)個粒子的位置和速度進行重置；smax＝8～10；

(6)在一個子群中，fitness_1為該子群中最大的適應度函數值，fitness_2為該子群中第二大的適應度函數值，tol為搜索精度，tol＝0.01，若滿足式(9)：

fitness_1-fitness_2<tol(9)

則將第二大的適應度函數值的粒子q的位置按照式(10)處理：

x'qd＝xqd+η·rand(10)

其中，xqd為粒子q原本的第d維位置，η為擾動因子，rand為0到1之間的隨機數，x'qd為粒子q擾動以后的第d維位置；擾動因子η的大小為：

η＝0.05(xmax-xmin)(11)

其中，xmax，xmin為粒子的搜索上下限，xmin＝0；

(7)確定種群的進化狀態；首先，定義每個粒子與其所在子群的子群中心的距離的絕對值之和dg：

其中，pig＝(pig1,pig2,...,pig(n+2))為粒子i所在子群的子群中心的位置；其次，定義每個粒子與其所在子群的子群中心的距離之和的絕對值dg：

定義進化因子δ為：

由定義可知進化因子δ∈[0,1]；

(8)按照式(15)(16)更新每個粒子的速度與位置：

vid(t)＝w·vid(t-1)+c1·rand·(pid-xid(t-1))+c2·rand·(pigd-xid(t-1))(15)

xid(t)＝xid(t-1)+vid(t)(16)

其中，w為慣性權重；c1,c2為加速因子，c1＝c2＝2；rand為0到1之間的隨機數；pi＝(pi1，pi2,...,pi(n+2))為粒子xi的歷史最優位置；pig＝(pig1，pig2,...,pig(n+2))為粒子i所在的子群的最優粒子的位置；慣性權重按照式(17)變換：

更新后，當d＝1,2,...,n+1時，若xid<0，則令xid＝0，若則令當d＝n+2時，若xid<500，則令xid＝500，若xid>700，則令xid＝700；

(9)迭代計數累加，t＝t+1.

(10)重復步驟(1)～(9)，直到達到最大迭代次數tmax停止迭代，tmax＝100～2000；

種群全局最優粒子pbest＝(pbest1,pbest2,...,pbest(n+2))所在的位置即優化后的n+1個節點的推力方向角和終端時刻；將全局最優粒子的位置信息輸入仿真模塊，按照式(2)、(3)、(4)獲得優化后的月球軟著陸軌道，月球軟著陸最優軌道規劃完成；

仿真模塊將最優軟著陸軌道通過實時通訊傳遞給執行模塊的執行元件執行，實現燃料消耗最少的月球軟著陸最優控制。

本發明的有益效果主要表現在：用直接離散法將軌道控制問題轉化為參數優化問題，使優化過程變得簡單易行；改進的智能優化方法控制了子群的大小，并且添加了擾動因子，增加了搜索的多樣性；根據進化狀態自適應變化的慣性權重提高了算法的收斂性能。本控制器具有很強的搜索能力，能夠尋找到軟著陸軌道的最優參數并且實現使燃料消耗最少的月球軟著陸最優控制。

附圖說明

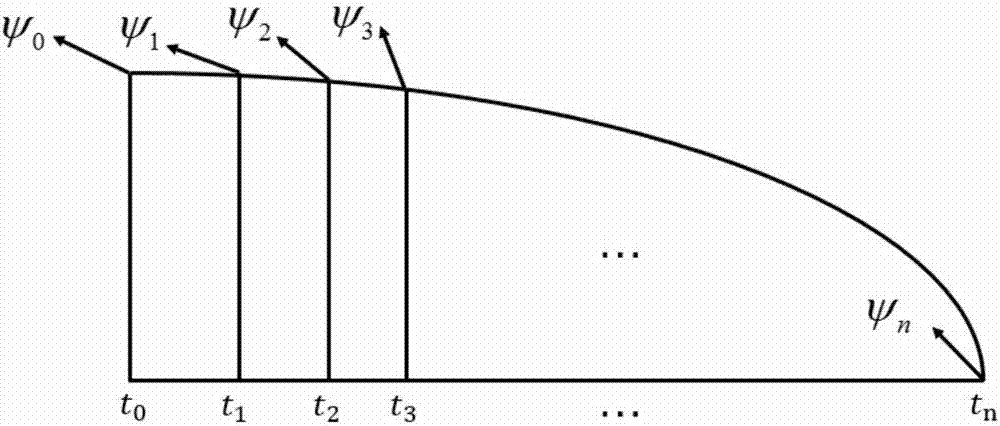
圖1是軌道離散化圖；

圖2是月球軟著陸極坐標系；

圖3是本發明的結構圖；

圖4是本發明的流程圖；

圖5是本發明中慣性權重w隨進化因子δ的變化圖。

具體實施方式

下面根據附圖以一個實例具體說明本發明。

一種自適應的月球軟著陸軌道快速優化控制器，參照圖3，該軌道快速優化控制器由優化模塊、仿真模塊、執行模塊組成；其中：

參照圖1，仿真模塊把月球軟著陸軌道分割成n個小段，本實例中令n取9，并將n的值輸入優化模塊。每個節點的時刻由式(1)得到：

其中，tk為第k+1個節點的時刻，k＝0,1,...,9，t0為初始時間，記t0＝0。

優化模塊把包括初始節點和終節點在內的10個節點的推力方向角ψ與軟著陸終端時刻tf作為待優化的參數。初始化種群規模為ns的粒子群，隨機生成維度為11的粒子i的初始位置xi＝(xi1,xi2,...,xi11)和初始速度vi＝(vi1,vi2,...,vi11)，i＝1,2,...,ns，并將粒子的位置信息傳入仿真模塊。定義維度變量d，d＝1,2,...,11。當d＝1,2,...,10時，xid代表第d個節點的推力方向角，由經驗可知軟著陸過程中推力方向角不會超過因此當d＝11時，xi11代表軟著陸終端時刻，根據實際情況軟著陸所花時間為500秒至700秒，因此xi11∈[500,700]，vi11∈[-200,200]。種群規模ns＝300～600。然后按以下方法進行迭代，初始時迭代計數t＝0：

(1)仿真模塊中，月球軟著陸過程中推力方向角表示成多項式(2)：

ψ(t)＝λ0+λ1t+λ2t²+λ3t³(2)

其中ψ(t)表示著陸軌道t時刻的推力方向角，λ0,λ1,λ2,λ3為系數，無實際意義。優化模塊輸入的粒子的位置代表10個節點的推力方向角及軟著陸終端時刻，按照式(1)得到10個節點的對應時刻。采用函數逼近法，利用10個節點的推力方向角及其對應時刻，對式(2)進行擬合，可以求得多項式的系數λ0,λ1,λ2,λ3，進而得到整個著陸軌道各個時刻的推力方向角ψ(t)。

(2)仿真模塊存儲了月球軟著陸時著陸器的質心動力學方程，見式(3)：

參照圖2，式(3)中r為著陸器的月心距離，v為著陸器的徑向速度，θ為著陸器極角，ω為著陸器極角角速度，μ為月球引力常數，m為著陸器質量，f為制動發動機推力，isp為制動發動機比沖。其中月球引力常數μ為常數，μ＝4902.75km³/s²，制動發動機推力f與制動發動機比沖isp與實際使用的發動機有關，也為常數。著陸器初始質量m0根據實際確定。本實例中f＝1350n，isp＝2940m/s，m0＝600kg。其他參數在著陸器著陸過程中發生變化。

由于起點處于霍曼轉移軌道的近地點，故初始條件為：

其中，rp和ra分別為霍曼轉移段的近地點半徑和遠地點半徑，rp＝1753km，ra＝1838km。

將步驟(1)中擬合得到的推力方向角ψ(t)、式(4)的初始條件以及著陸器初始質量m0帶入動力學方程(3)，所有數據單位統一，獲得月球軟著陸的軌道，并將獲得的軌道信息輸入給優化模塊。

(3)優化模塊中，優化目標為軟著陸過程消耗燃料最少，即令式(5)中指標j最大：

同時，為實現軟著陸，終端約束條件為：

其中，r為月球半徑，r＝1738km。

在適應度函數中考慮約束條件，構造適應度函數fitness：

fitness＝j-α[(r(tf)-r)²+v²(tf)+ω²(tf)](7)

其中r(tf)、v(tf)、ω(tf)分別表示仿真模塊輸入的軟著陸軌道終端時刻的月心距離、徑向速度、極角角速度。α為罰因子，罰因子應足夠大，令α＝10000。適應度函數值越大，說明消耗的燃料越少，規劃的軌道越優。若規劃的軌道不滿足終端約束，則適應度函數值將會變得很小。根據仿真模塊輸入的軟著陸軌道，按照式(7)計算適應度函數值。適應度函數值最大的粒子為全局最優粒子，其位置為pbest＝(pbest1,pbest2,...,pbest11)。

(4)在優化模塊中對所有粒子進行分群操作，包括以下子步驟：

(4.1)將所有粒子按照適應度函數值大小從大到小排序，選取適應度函數值最大的粒子作為一個子群中心；

(4.2)在剩下的粒子中選取適應度函數值最大的粒子，依次計算該粒子與各個子群中心的歐幾里得距離。粒子i與粒子j的歐幾里得距離dist(i,j)定義為：

其中，xi＝(xi1,xi2,...,xi11)代表粒子i的位置，xj＝(xj1,xj2,...,xj11)代表粒子j的位置，i,j＝1,2,...,ns。若該粒子與某一個子群中心的歐幾里得距離小于半徑r，則將該粒子歸為該子群中心所在的子群，并不再計算該粒子與剩下的子群中心的歐幾里得距離；若該粒子與所有子群中心的距離都大于半徑r，則將該粒子置為一個新的子群中心。根據搜索空間的大小，本實例中半徑r＝20。

(4.3)重復步驟4.2)，直到處理完所有粒子，則分群完成，且每個子群中心為該子群中適應度函數值最大的粒子。

(5)檢查每個子群中的粒子數，若一個子群中的粒子數為s，且s>smax，smax為子群允許的最大粒子數，則將適應度最差的(s-smax)個粒子的位置和速度進行重置。這樣做的目的是防止一個子群中包含過多的粒子而導致搜索多樣性下降。增加搜索過程的多樣性能增大算法搜索到全局最優的概率從而規劃出更優的軌道。在一個子群范圍內，粒子數不需要太多，本實例中令smax＝10。

(6)在一個子群中，fitness_1為該子群中最大的適應度函數值，fitness_2為該子群中第二大的適應度函數值，tol為搜索精度，tol＝0.01，若滿足式(9)：

|fitness_1-fitness_2|<tol(9)

則說明這兩個粒子的適應度函數值過分接近，將第二大的適應度函數值的粒子q的位置按照式(10)處理：

x'qd＝xqd+η·rand(10)

其中，xqd為粒子q原本的第d維位置，η為擾動因子，rand為0到1之間的隨機數，x'qd為粒子q擾動以后的第d維位置。添加擾動因子可以增加搜索的多樣性，從而規劃出更優的軌道。但是擾動因子過大又會影響粒子群的正常更新，因此設擾動因子η的大小為：

η＝0.05(xmax-xmin)(11)

其中，xmax，xmin為粒子的搜索上下限，xmin＝0。

(7)確定種群的進化狀態。隨著粒子的更新，種群共經歷四種進化狀態，即探索期、開拓期、聚合期以及跳出期。下面利用進化因子來表示進化狀態。首先，定義每個粒子與其所在子群的子群中心的距離的絕對值之和dg：

其中，pig＝(pig1,pig2,...,pig11)為粒子i所在子群的子群中心的位置。其次，定義每個粒子與其所在子群的子群中心的距離之和的絕對值dg：

在進化初始階段，dg取值略小于dg；在進化收斂階段，dg取值遠小于dg；在跳出階段，dg取值接近于dg。因此，定義進化因子δ為：

由定義可知進化因子δ∈[0,1]。

(8)按照式(15)(16)更新每個粒子的速度與位置：

vid(t)＝w·vid(t-1)+c1·rand·(pid-xid(t-1))+c2·rand·(pigd-xid(t-1))(15)

xid(t)＝xid(t-1)+vid(t)(16)

其中，w為慣性權重；c1,c2為加速因子，c1＝c2＝2；rand為0到1之間的隨機數；pi＝(pi1，pi2,...,pi11)為粒子xi的歷史最優位置；pig＝(pig1，pig2,...,pig11)為粒子i所在的子群的最優粒子的位置。

慣性權重w越大，算法的搜索能力越強，反之亦然。在探索期，希望慣性權重大一些，在聚合期，希望慣性權重小一些。由于進化因子可以反映進化狀態，參照圖5，慣性權重按照式(17)變換：

其中，δ為進化因子。由于進化因子δ∈[0,1]，因此慣性權重w∈[0.4,0.9]。進化因子大，表示為初始階段，大的慣性權重能擴大搜索范圍；進化因子小，表示為收斂階段，小的慣性權重能精確搜索。跟隨進化狀態而變化的慣性權重能夠根據實際情況隨時調整，提高了算法的搜索能力與收斂速度。

更新后，當d＝1,2,...,10時，若xid<0，則令xid＝0，若則令當d＝11時，若xi11<500，則令xi11＝500，若xi11>700，則令xi11＝700。

(9)迭代計數累加，t＝t+1.

(10)重復步驟(1)～(9)，直到達到最大迭代次數tmax停止迭代，本實例中tmax＝500。

種群全局最優粒子pbest＝(pbest1,pbest2,...,pbest11)所在的位置即優化后的10個節點的推力方向角和終端時刻。將全局最優粒子的位置信息輸入仿真模塊，按照式(2)、(3)、(4)獲得優化后的月球軟著陸軌道，月球軟著陸最優軌道規劃完成。

仿真模塊將最優軟著陸軌道通過實時通訊傳遞給執行模塊的執行元件執行，實現燃料消耗最少的月球軟著陸最優控制。

上述實施例用來解釋說明本發明，而不是對本發明進行限制，在本發明的精神和權利要求的保護范圍內，對本發明作出的任何修改和改變，都落入本發明的保護范圍。