本發明公開了一種計算Timoshenko梁高階自然頻率準確解的方法，具體涉及梁類結構動力特性分析領域。

背景技術：

梁類結構作為最常見的一類基本結構，準確獲取其動力特性，尤其是自然頻率是工程中較為關心的問題，同時梁的高階振動問題在機械、航空航天領域都至關重要。Timoshenko梁理論是一種適用于梁高階自然頻率計算的梁理論，通過在梁一端建立一個坐標系，建立4個邊界條件方程，得到4階齊次線性方程組，可以計算得到Timoshenko梁較高階(通常小于12階)自然頻率的準確解。但由于普通計算機數值計算精度的限制，無法獲得更高階自然頻率的準確解，只能通過其他數值方法得到其近似解。基于這樣的考慮，需要考慮設計一種計算Timoshenko梁高階自然頻率準確解的方法。

技術實現要素：

本發明所要解決的技術問題是：針對現有計算Timoshenko梁自然頻率準確解的方法中，由于數值計算條件的限制，無法獲得更高階自然頻率的準確解的問題，提出建立一種計算Timoshenko梁高階自然頻率準確解的方法。

本發明為解決上述技術問題采用以下技術方案：

本發明提出一種計算Timoshenko梁高階自然頻率準確解的方法，包括如下步驟：

一種計算Timoshenko梁高階自然頻率準確解的方法，包括如下步驟：

(1)、在梁長度方向上建立n個局部坐標系，通過局部坐標系將梁分成n個梁段，建立各梁段的橫向位移以及彎曲引起的截面轉角的統一計算表達式，n為大于1的自然數；

(2)、在相鄰兩個梁段之間分別建立位移、轉角、彎矩和剪力的連續性條件方程，n個梁段共得到4n-4個連續性條件方程；根據梁的邊界類型，在梁兩端建立4個邊界條件方程；

(3)、將各梁段的橫向位移以及彎曲引起的截面轉角分別對應代入步驟(2)建立的4n-4個連續性條件方程和4個邊界條件方程，得到4n階齊次線性方程組，然后通過依次賦值圓頻率并代入4n階齊次線性方程組中求解Timoshenko梁的各階自然頻率。

進一步的，本發明提出的計算Timoshenko梁高階自然頻率準確解的方法，步驟(1)中，設第i個梁段的長度為S_i，梁長i＝1,2，...,n-1；在每個梁段局部坐標系中橫坐標為x_i，無量綱橫坐標ζ_i＝x_i/S_i，0≤ζ_i≤1；則第i個梁段的橫向位移W_i(ζ)和彎曲引起的截面轉角ψ_i(ζ)分別為：

W_i(ζ_i)＝A_i cosh(γ₁S_iζ_i/L)+B_i sinh(γ₁S_iζ_i/L)+C_i cos(γ₂S_iζ_i/L)+D_i sin(γ₂S_iζ_i/L)

ψ_i(ζ_i)＝A_im₁ sinh(γ₁S_iζ_i/L)+B_im₁ cosh(γ₁S_iζ_i/L)+C_im₂ sin(γ₂S_iζ_i/L)-D_im₂cos(γ₂S_iζ_i/L)

其中s＝θr，β＝τ(τrs-1)，E為其彈性模量，G為剪切模量，I為截面慣性矩，ρ為材料密度，A為截面面積，k為截面剪切系數，ω為圓頻率，A_i,B_i,C_i,D_i分別為步驟(3)中待求未知數，sinh和cosh分別為雙曲正弦與雙曲余弦函數。

進一步的，本發明提出的計算Timoshenko梁高階自然頻率準確解的方法，步驟(2)是在相鄰的第i個梁段和第i+1個梁段連接處建立位移、轉角、彎矩和剪力的連續性條件方程，分別如下:

位移的連續性條件方程為：

轉角的連續性條件方程為：

彎矩的連續性條件方程為：

剪力的連續性條件方程為：

其中，W_i'(ζ_i)、ψ_i'(ζ_i)分別代表橫向位移W_i(ζ)的斜率和轉角ψ_i(ζ)的斜率。

進一步的，本發明提出的計算Timoshenko梁高階自然頻率準確解的方法，每個梁端邊界條件由以下4個邊界條件方程中任意兩個方程組合得到：

W(ζ)＝0

ψ(ζ)＝0

ψ'(ζ)＝0

W'(ζ)-ψ(ζ)＝0；

其中，ζ₁＝0，ζ_n＝1。

進一步的，本發明提出的計算Timoshenko梁高階自然頻率準確解的方法，三種常見的梁端邊界條件如下：固定端邊界條件為W(ζ)＝0和ψ(ζ)＝0，自由端邊界條件為ψ'(ζ)＝0和W'(ζ)-ψ(ζ)＝0，簡支端邊界條件為W(ζ)＝0和ψ'(ζ)＝0。

進一步的，本發明提出的計算Timoshenko梁高階自然頻率準確解的方法，將步驟(2)中橫向位移W_i(ζ)和彎曲引起的截面轉角ψ_i(ζ)代入4n-4個連續性方程和4個邊界條件方程，得到以A_i,B_i,C_i,D_i為未知數的4n階齊次線性方程組。

進一步的，本發明提出的計算Timoshenko梁高階自然頻率準確解的方法，步驟(3)中求解自然頻率方法為：

在求解范圍內依次賦值圓頻率ω并代入齊次線性方程組的系數矩陣D(ω)，由其行列式|D(ω)|得到Y(ω)，

第j個令Y(ω)等于零的ω的值，即為梁的第j個自然頻率。

本發明采用以上技術方案與現有技術相比，具有以下技術效果：

本發明公開了一種計算Timoshenko梁高階自然頻率準確解的方法，該方法能突破現有計算Timoshenko梁高階自然頻率準確解的瓶頸，極大地擴展求解范圍，實現Timoshenko梁高階自然頻率準確解的計算。

附圖說明

圖1是本發明的局部坐標下的梁示意圖。

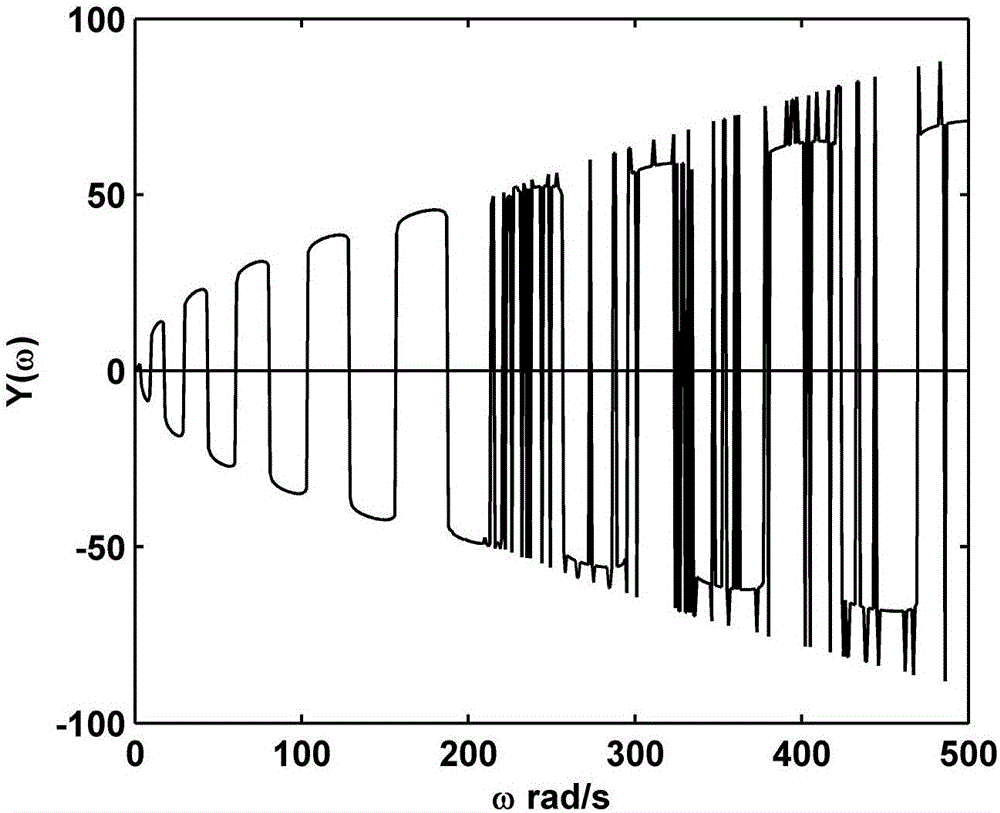
圖2是使用現有技術的Timoshenko梁自然頻率求解結果圖。

圖3是使用本發明的Timoshenko梁自然頻率求解結果圖。

圖4是本發明的方法流程圖。

具體實施方式

下面結合附圖對本發明的技術方案做進一步的詳細說明：

本技術領域技術人員可以理解的是，除非另外定義，這里使用的所有術語(包括技術術語和科學術語)具有與本發明所屬領域中的普通技術人員的一般理解相同的意義。還應該理解的是，諸如通用字典中定義的那些術語應該被理解為具有與現有技術的上下文中的意義一致的意義，并且除非像這里一樣定義，不會用理想化或過于正式的含義來解釋。

首先，如圖4所示，本發明提出一種計算Timoshenko梁高階自然頻率準確解的方法，包括如下步驟：

(1)、如圖1所示，在梁長度方向上建立n個局部坐標系，通過局部坐標系將梁分成n個梁段；第i個梁段的長度為S_i，梁長i＝1,...,n-1；在每個梁段局部坐標系中橫坐標為x_i，無量綱橫坐標ζ_i＝x_i/S_i，0≤ζ_i≤1；則第i個梁段的橫向位移W_i(ζ)和彎曲引起的截面轉角ψ_i(ζ)分別為：

W_i(ζ_i)＝A_i cosh(γ₁S_iζ_i/L)+B_i sinh(γ₁S_iζ_i/L)+C_i cos(γ₂S_iζ_i/L)+D_i sin(γ₂S_iζ_i/L)，

ψ_i(ζ_i)＝A_im₁ sinh(γ₁S_iζ_i/L)+B_im₁ cosh(γ₁S_iζ_i/L)+C_im₂ sin(γ₂S_iζ_i/L)-D_im₂cos(γ₂S_iζ_i/L)，

其中s＝θr，β＝τ(τrs-1)，E為其彈性模量，G為剪切模量，I為截面慣性矩，ρ為材料密度，A為截面面積，k為截面剪切系數，ω為圓頻率，A_i,B_i,C_i,D_i分別為步驟(3)中待求未知數，sinh和cosh分別為雙曲正弦與雙曲余弦函數。

(2)、在相鄰兩個梁段之間建立位移、轉角、彎矩和剪力的連續性條件方程，得到4n-4個方程；具體的，相鄰的第i個梁段和第i+1個梁段連接處建立位移、轉角、彎矩和剪力的連續性條件方程分別如下:

一端固支，一端自由的4個邊界條件方程具體為：

一端固定，一端簡支的4個邊界條件方程具體為：

兩端簡支的4個邊界條件方程具體為：

(3)、將橫向位移W_i(ζ)和彎曲引起的截面轉角ψ_i(ζ)代入4n-4個連續性方程和4個邊界條件方程，得到以A_i,B_i,C_i,D_i為未知數的4n階齊次線性方程組，求解Timoshenko梁各階自然頻率。

齊次線性方程組為D(ω)C＝0

其中待求未知數向量C＝(A₁,B₁,C₁,D₁,A₂,B₂,C₂,D₂,...,A_n,B_n,C_n,D_n)^T

系數矩陣

P_i＝(P_i,1 P_i,2)

對于一端固支，一端簡支的邊界條件：

對于一端固支，一端簡支的邊界條件：

對于兩端簡支的邊界條件：

(3)、在求解范圍內依次賦值圓頻率ω并代入齊次線性方程組的系數矩陣D(ω)中，由其行列式|D(ω)|得到Y(ω)，

第j個令Y(ω)等于零的ω的值，即為梁的第j個自然頻率。

下面具體舉例說明本發明的技術方案，本實施例所用矩形截面懸臂梁(一端固支，一端自由)彈性模量為70Mpa，剪切模量為26.3Mpa，截面剪切系數為0.851，密度為2700kg/m³，長度為1m，截面尺寸為0.01m×0.01m。

首先，根據步驟(1)在梁長度方向上建立4個局部坐標系，通過局部坐標系將梁分成4個梁段，每個梁段長度為0.25m。

其次，根據步驟(2)-(3)在相鄰的第i(i＝1,2,3)個梁段和第i+1個梁段連接處建立12個位移、轉角、彎矩和剪力的連續性條件方程:

和4個邊界條件方程：

得到16階齊次線性方程組。

最后，從0到500rad/s依次賦值圓頻率ω并代入系數矩陣D(ω)中，由其行列式|D(ω)|得到Y(ω)，

第j個令Y(ω)等于零的ω的值，即梁的第j個自然頻率。

圖2為使用現有技術的Timoshenko梁自然頻率求解結果圖，圖3為使用本發明的Timoshenko梁自然頻率求解結果圖，使用現有技術和使用本發明得到的Timoshenko梁自然頻率如表1所列，對比結果可以發現使用現有技術只能計算Timoshenko梁前11階自然頻率，之后就會出現數值計算錯誤，而使用本發明提出的一種計算Timoshenko梁高階自然頻率準確解的方法，可以有效計算至少前18階自然頻率。

表1

以上所述僅是本發明的部分實施方式，應當指出，對于本技術領域的普通技術人員來說，在不脫離本發明原理的前提下，還可以做出若干改進和潤飾，這些改進和潤飾也應視為本發明的保護范圍。