一種基于遺傳蟻群融合算法的數字微流控芯片災難性故障測試方法與流程
本發明涉及數字微流控芯片測試技術,具體是一種基于遺傳蟻群融合算法的數字微流控芯片災難性故障測試方法。
背景技術:
數字微流控芯片常用于臨床檢測、醫藥工程等對可靠性要求高的領域,因此需要對數字微流控芯片進行全面且高效的測試,保證其可靠性。數字微流控芯片的故障可分為災難性故障和參數性故障,災難性故障又可細分為絕緣體擊穿、相鄰電極短路、電極板斷路等故障。災難性故障對芯片的破壞性是致命的,會導致芯片上實驗液滴的完全停滯,使芯片無法正常工作。因此,對災難性故障的測試是數字微流控芯片測試工作中特別重要的一步。
數字微流控芯片的災難性故障測試原理為:利用測試液滴遍歷數字微流控芯片的陣列單元,若無故障,則測試液滴在遍歷后能夠到達數字微流控芯片上的廢液池,若存在故障,則會導致測試液滴在數字微流控芯片上的停滯,測試液滴無法到達數字微流控芯片上的廢液池。廢液池處有檢測液滴是否到達的檢測電路,若檢測電路檢測到測試液滴的到達,則說明數字微流控芯片無故障,否則,說明存在故障。測試液滴遍歷數字微流控芯片的陣列單元的不同路由次序就形成了不同的測試路徑,測試路徑越短則測試花費的時間就越少,測試效率越高。另外,測試算法本身的復雜度越低、收斂性越好,則測試算法的執行效率越高,更有利于算法的在實際工作中的執行。
目前,針對數字微流控芯片的災難性故障,已有多種測試方法,如漢密爾頓回路測試法、歐拉回路測試法、并行掃描測試法、內建自測試法、分區子陣列合并調度測試法、基于蟻群算法的搜索測試路徑的方法等。在這些方法中,漢密爾頓回路測試法、分區子陣列合并調度測試法無法檢測出相鄰電極短路故障;并行掃描測試法、內建自測試法只適用于規則矩形陣列的數字微流控芯片的測試,且在線測試效率較低;歐拉回路測試法在應用大規模芯片測試時算法復雜度較高且在線測試效率較低;基于蟻群算法的搜索測試路徑的方法,測試模型的建立步驟較繁瑣,且單一的蟻群算法收斂性較差,在應用大規模芯片測試時效率較低。
技術實現要素:
本發明目的是針對技術中的不足,而提供一種基于遺傳蟻群融合算法的數字微流控芯片災難性故障測試方法。這種測試方法不但能改善單一蟻群算法收斂性差的問題,而且提高測試算法的執行效率,并且能快速求得測試路徑,這種測試方法能夠檢測出相鄰電極短路故障,且兼容規則與非規則陣列芯片的測試,更有利于應用于大規模芯片的測試。
實現本發明目的的技術方案是:
一種基于遺傳蟻群融合算法的數字微流控芯片災難性故障測試方法,與現有技術不同的是,包括以下步驟:
S1.建立數字微流控芯片的災難性故障測試模型:根據數字微流控芯片的陣列單元結構,建立數字微流控芯片的災難性故障測試模型,所述模型為:
(1)把數字微流控芯片的陣列單元抽象為無向圖G(V,E)的頂點V,相鄰陣列單元之間的連接關系抽象為無間圖G(V,E)的邊E,得到無間圖模型G(V,E),并建立其對應的鄰接矩陣A;
(2)對無向圖模型G(V,E)中的所有頂點V進行編號,令每個頂點的編號對應為該頂點在鄰接矩陣A中的行號,從編號最小的頂點開始,依次搜索與當前頂點相關聯的邊,并對搜索到的邊從小到大進行編號;
(3)將無向圖模型G(V,E)中的邊E抽象為無向圖模型G′(V′,E′)的頂點V′,并令頂點V′的編號一一對應G(V,E)中邊E的編號,將無向圖模型G(V,E)中邊E之間的鄰接關系抽象為無向圖模型G′(V′,E′)的邊E′,建立無向圖模型G′(V′,E′)及其對應的鄰接矩陣B;
(4)采用改進的Floyd方法計算無向圖模型G′(V′,E′)中任意兩頂點間的最短路徑,以兩頂點間的最短路徑作為兩頂點間邊的權值,構造一個完全連通圖模型G″(V″,E″),以此完全連通圖模型G″(V″,E″)作為數字微流控芯片災難性故障測試的模型;
S2.得到初步測試路徑并設置最大最小蟻群算法的初始信息素上下界和信息素初始值:根據數字微流控芯片災難性故障測試模型G″(V″,E″),采用遺傳算法得到初步測試路徑,并根據初步測試路徑設置最大最小蟻群算法的初始信息素上下界和信息素初始值,其中,初始信息素上下界和信息素初始值具體設置公式為:
其中,τmax(0)、τmin(0)分別為初始信息素上界和下界,是遺傳算法求得的初步測試路徑中最短測試路徑的長度,Pbest表示蟻群算法收斂時構造最優解的概率,avg等于m/2,m是最大最小蟻群算法中設置的螞蟻數量,ρ是信息素殘留系數,τij(0)為任意路徑(i,j)上的信息素初值,u表示從遺傳算法求得初步測試路徑中選擇最短的u個測試路徑,是遺傳算法求得的初步測試路徑中的一個測試路徑k的長度;
S3.搜索最終測試路徑并輸出結果:根據數字微流控芯片災難性故障測試模型G″(V″,E″)和步驟S2得到的初始信息素上下界和信息素初始值,采用最大最小蟻群算法搜索最終測試路徑,蟻群算法迭代完成后,輸出最終測試路徑,其中,最大最小蟻群算法的目標函數為:
其中,為最終測試路徑中兩個相鄰路由節點v″i和v″i+1之間的距離權值,路由節點v″i和v″i+1即為數字微流控芯片災難性故障測試模型G″(V″,E″)中的兩個頂點。
所述步驟S1中的改進Floyd方法為:
在計算無向圖G′(V′,E′)中任意兩頂點v′i和v′j之間最短路徑時,先對待插入的節點v′r進行路長比較,如果dir≥dij或drj≥dij,dij代表兩個頂點之間的距離,則說明插入節點v′r后,v′i經過v′r到達v′j的路徑不會比原來兩頂點之間的路徑短,于是不再計算dir+drj,直接進行下一節點的搜索,且無向圖G′(V′,E′)中頂點v′i到v′j的距離與v′j到v′i的距離對稱相等,若已計算v′i到v′j的距離,則不需再計算v′j到v′i的距離,這樣做減少了計算量。
所述步驟S2中遺傳算法的染色體編碼方案采用十進制整數編碼,以初步測試路徑的一個路由節點次序作為一條染色體,且染色體編碼的起始位代表數字微流控芯片上液滴源所在的位置,編碼末位代表數字微流控芯片上廢液池所在的位置。
所述步驟S2中的遺傳算法的選擇算子采用適應度比例方法,交叉算子采用順序交叉法,變異算子采用逆轉變異方法,且染色體起始位和末位不參與交叉操作和變異操作。
所述步驟S3中的最大最小蟻群算法在搜索最終測試路徑時,按照偽隨機比例規則搜索最終測試路徑的節點,具體地,螞蟻按照下面的公式搜索最終測試路徑的節點:
其中,q0∈(0,1)是常數,q∈(0,1)是隨機數,τij(t)表示t時刻節點v″i和v″j間的信息素,ηij(t)表示啟發信息,ηij(t)=1/dij,dij為數字微流控芯片災難性故障測試模型G″(V″,E″)中兩節點v″i和v″j間的距離,α和β分別表示影響信息素和啟發信息的相對強弱的兩個參數。
所述步驟S3中最大最小蟻群算法的信息素更新策略為:只允許每次迭代后的最短測試路徑增加信息素,具體地,信息素按照下面的公式更新:
其中,ρ是信息素殘留系數,Δτij(t)表示路徑(i,j)上的信息素增量。f(Sbest)為本次最大最小蟻群算法迭代中最短測試路徑的長度Lls或當前全局最短測試路徑的長度Lgs。
所述步驟S3中的最大最小蟻群算法的信息素上下界采用動態更新策略,具體地,信息素上下界更新公式如下:
其中,τmax(t)、τmin(t)為t時刻信息素的上下界,Lls為本次最大最小蟻群算法迭代后最短測試路徑的長度。
所述步驟S3中采用最大最小蟻群算法搜索最終測試路徑時,為了防止液滴之間的意外融合,測試液滴需要滿足靜態約束條件和動態約束條件。
這種測試方法不但改善了單一蟻群算法收斂性差的問題,而且提高了測試算法的執行效率,并且能快速求得測試路徑。這種測試方法能夠檢測出相鄰電極短路故障,且兼容規則陣列與非規則陣列數字微流控芯片,更有利于應用于大規模數字微流控芯片的災難性故障測試。
附圖說明
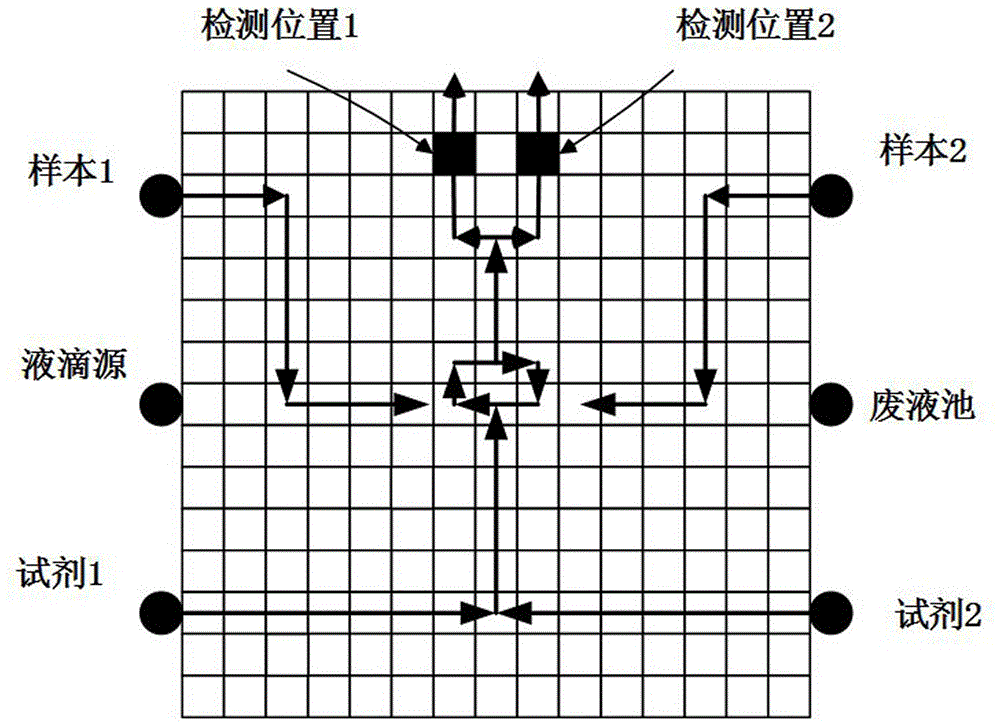
圖1為實施例多元生化實驗的數字微流控芯片的結構示意圖;
圖2為一個3×3規則陣列數字微流控芯片的災難性故障測試模型轉換示意圖;
圖3為數字微流控芯片上液滴之間的約束條件示意圖;
圖4為實施例方法應用于多元生化實驗數字微流控芯片的災難性故障測試的方法收斂示意圖;
圖5為實施例方法與歐拉回路法、蟻群測試算法分別應用于多元生化實驗數字微流控芯片的災難性故障測試所花費的測試時間對比示意圖;
圖6為實施例方法的流程示意圖。
具體實施方式
下面結合附圖和實施例對本發明內容作進一步的闡述,但并不是對本發明的限定。
實施例:
參照圖6,一種基于遺傳蟻群融合算法的數字微流控芯片災難性故障測試方法,包括以下步驟:
S1.建立數字微流控芯片的災難性故障測試模型:根據數字微流控芯片的陣列單元結構,建立數字微流控芯片的災難性故障測試模型,所述模型為:
(1)把數字微流控芯片的陣列單元抽象為無向圖G(V,E)的頂點V,相鄰陣列單元之間的連接關系抽象為無向圖G(V,E)的邊E,得到無向圖模型G(V,E),并建立其對應的鄰接矩陣A;
(2)對無向圖模型G(V,E)中的所有頂點V進行編號,令每個頂點的編號對應為該頂點在鄰接矩陣A中的行號,從編號最小的頂點開始,依次搜索與當前頂點相關聯的邊,并對搜索到的邊從小到大進行編號;
(3)將無向圖模型G(V,E)中的邊E抽象為無向圖模型G′(V′,E′)的頂點V′,并令頂點V′的編號一一對應G(V,E)中邊E的編號,將無向圖模型G(V,E)中邊E之間的鄰接關系抽象為無向圖模型G′(V′,E′)的邊E′,建立無向圖模型G′(V′,E′)及其對應的鄰接矩陣B;
(4)采用改進的Floyd方法計算無向圖模型G′(V′,E′)中任意兩頂點間的最短路徑,以兩頂點間的最短路徑作為兩頂點間邊的權值,構造一個完全連通圖模型G″(V″,E″),以此完全連通圖模型G″(V″,E″)作為數字微流控芯片災難性故障測試的模型;
如圖1所示的多元生化實驗的數字微流控芯片,該數字微流控芯片有一個測試液滴源和一個廢液池,圖中的箭頭方向為實驗液滴的移動路徑,檢測位置1和2是檢測實驗液滴反應結果的位置,為了對其進行災難性故障測試,需要測試液滴從液滴源出發遍歷整個數字微流控芯片后到達廢液池,為了防止液滴之間的意外融合,測試液滴之間需要滿足靜態約束條件和動態約束條件,該數字微流控芯片陣列單元數為225個,數量較大,因此為了對測試模型轉化的過程進行直觀的說明,參照圖2的3×3規則陣列的數字微流控芯片,具體為:
(1)把3×3規則陣列的數字微流控芯片的陣列單元抽象為無向圖模型G(V,E)中的頂點V,陣列單元的相鄰關系抽象為邊E,得到如圖2中所示的無向圖模型G(V,E),并建立與無向模型G(V,E)對應的鄰接矩陣A;
(2)對圖2所示的無向圖模型G(V,E)中頂點V進行編號,頂點的編號對應為頂點在鄰接矩陣A的行號,從編號最小的頂點開始,依次搜索與當前頂點相關聯的邊,并對搜索到的邊從小到大進行編號,如圖2所示無向圖模型G(V,E)中邊E的編號為“1”到“12”;
(3)將無向圖模型G(V,E)中的邊E抽象為將無向圖模型G′(V′,E′)的頂點V′,將無向圖模型G(V,E)中邊E之間的鄰接關系抽象為無向圖模型G′(V′,E′)的邊E′,得到無向圖模型G′(V′,E′),所述無向圖模型G(V,E)中邊E之間的鄰接關系為:若無向圖模型G(V,E)中的兩條邊有共同頂點,說明這兩條邊是鄰接的,則其對應的無向圖模型G′(V′,E′)中的頂點之間存在一條邊,如附圖2所示將無向圖G(V,E)中編號為“11”和“12”的邊抽象為無向圖G′(V′,E′)的頂點,編號為“11”和“12”的兩條邊存在共同的頂點,則其抽象為圖G′(V′,E′)中的兩個頂點之間存在一條邊;
(4)最后根據無向圖模型G′(V′,E′),利用改進的Floyd方法計算G′(V′,E′)中任意兩頂點間的最短路徑,以兩頂點之間最短路徑作為兩頂點間邊的權值,構造一個完全連通圖模型G″(V″,E″),以此完全連通圖模型G″(V″,E″)作為數字微流控芯片災難性故障測試的模型。如圖2所示的3×3規則陣列數字微流控芯片轉化的完全連通圖G″(V″,E″)中有12個頂點,則其對應條邊,由于邊數太多無法直觀畫出來,故測試模型轉換中沒有給出完全連通圖G″(V″,E″)的具體圖形。
上述步驟S1中數字微流控芯片災難性故障測試模型的轉換方法適用于所有規則和非規則陣列的數字微流控芯片。
S2.得到初步測試路徑并設置最大最小蟻群算法的初始信息素上下界和信息素初始值:根據數字微流控芯片災難性故障測試模型G″(V″,E″)采用遺傳算法得到初步測試路徑,并根據初步測試路徑設置最大最小蟻群算法的初始信息素上下界和信息素初始值,其中,初始信息素上下界和信息素初始值具體設置公式為:
其中,τmax(0)、τmin(0)分別為初始信息素上界和下界,是遺傳算法求得的初步測試路徑中最短測試路徑的長度,Pbest表示蟻群算法收斂時構造最優解的概率,avg等于m/2,m是最大最小蟻群算法中設置的螞蟻數量,ρ是信息素殘留系數,τij(0)為任意路徑(i,j)上的信息素初值,u表示從遺傳算法求得初步測試路徑中選擇最短的u個測試路徑,是遺傳算法求得的初步測試路徑中的一個測試路徑k的長度;
具體為:
在遺傳算法迭代完成后,從遺傳算法求得的初步測試路徑中,選擇其中較短的初步測試路徑來計算最大最小蟻群算法的初始信息素上下界和信息素初始值,本實施例應用于多元生化實驗數字微流控芯片的災難性故障測試中,相關參數的優選的方案為:遺傳算法的迭代次數設為150次,種群的染色體數量N設為50,迭代完成后在求得的50條初步測試路徑中取前u=30條最短的初步測試路徑來形成初始信息素上下界和信息素初始值,取ρ=0.92,Pbest=0.05,螞蟻的數量m=30;
S3.搜索最終測試路徑并輸出結果:根據數字微流控芯片災難性故障測試模型G″(V″,E″)和步驟S2得到的初始信息素上下界和信息素初始值,采用最大最小蟻群算法搜索最終測試路徑,蟻群算法迭代完成后,輸出最終測試路徑,其中,最大最小蟻群算法的目標函數為:
其中,為最終測試路徑中兩個相鄰路由節點v″i和v″i+1之間的距離權值,路由節點v″i和v″i+1即為數字微流控芯片災難性故障測試模型G″(V″,E″)中的兩個頂點。
所述步驟S1中的改進Floyd方法為:
在計算無向圖G′(V′,E′)中任意兩頂點v′i和v′j之間最短路徑時,先對待插入的節點v′r進行路長比較,如果dir≥dij或drj≥dij,dij代表兩個頂點之間的距離,則說明插入節點v′r后,v′i經過v′r到達v′j的路徑不會比原來兩頂點之間的路徑短,于是不再計算dir+drj,直接進行下一節點的搜索,且無向圖G′(V′,E′)中頂點v′i到v′j的距離與v′j到v′i的距離對稱相等,若已計算v′i到v′j的距離,則不需再計算v′j到v′i的距離,這樣做減少了計算量。
具體的,改進后的Floyd方法的流程如下:
S2-1)從無向圖模型G′(V′,E′)中編號最小的頂點開始,搜索任意一對頂點v′i與v′j之間,是否存在另一個頂點v′r,使v′i經過v′r到v′j的距離比當前v′i到v′j的距離短,若是則更新v′i與v′j之間的距離,否則繼續搜索下一節點;比較距離時,可以對待插入的節點v′r先進行路長比較,如果dir≥dij或drj≥dij(dij代表兩個頂點之間的距離),則說明插入節點v′r后,v′i經過v′r到達v′j的路徑不會比原來兩點之間的路徑短,則直接進行下一節點的搜索;
S2-2)更新任意兩頂點之間的距離權值之后,得到一個完全連通圖G″(V″,E″)的鄰接矩陣C。在算法迭代過程中,由于v′i到v′j的距離與v′j到v′i的距離相等,若已更新v′i到v′j的距離,則不需再計算v′j到v′i的距離,可以提高Floyd方法的效率。
所述步驟S2中遺傳算法的染色體編碼方案采用十進制整數編碼,以測試路徑的一個路由節點次序作為一條染色體,且染色體編碼的起始位代表數字微流控芯片上液滴源所在的位置,編碼末位代表數字微流控芯片上廢液池所在的位置,染色體十進制整數編碼的方案為:
將測試模型G″(V″,E″)中頂點的十進制編號作為染色體的基因的編碼,如附圖2中所示的G″(V″,E″)中頂點編號為從“1”到“12”,則可以編碼染色體為(1-2-3-4-5-6-7-8-9-10-11-12)或任意其他情況的頂點編號的排列組合。
所述步驟S2中的遺傳算法的選擇算子采用適應度比例方法,交叉算子采用順序交叉法,變異算子采用逆轉變異方法,且染色體起始位和末位不參與交叉操作和變異操作,交叉操作和變異操作流程如下:
S2-3)利用遺傳算法求解測試路徑時,每一次迭代需要采用適應度比例方法從種群N中選擇M/2(M≥N)對染色體進行交叉操作。具體的,個體k被選擇的概率為:
fk=1/Lk
其中,fk為適應度函數,為染色體Xk代表的測試路徑中兩個相鄰節點xi和xi+1之間的距離,N為種群的染色體數量;本實施例中,M的一種優選值為80,N設為50。
S2-4)染色體選擇完成后,采用順序交叉法對選擇的M/2對染色體進行交叉操作,且測試路徑的起點和終點代表液滴源和廢液池,不參與交叉操作。本實施例中,附圖1所示數字微流控芯片陣列單元之間連接邊的數量為420,數量較大,不便于直觀說明交叉的具體操作。不失一般性,以10個基因的染色體為例,來直觀地說明順序交叉法的交叉過程如下:
①隨機在父串上選擇一個交叉區域,如兩父串和交叉區域為:
X1=x0x1x2|x3x4x5x6|x7x8x9
X2=x0x8x4|x7x6x2x1|x3x5x9
②將X2的交叉區加到X1中起點x0后面,同樣將X1的交叉區加到X2中起點x0后面,可得:
X′1=x0|x7x6x2x1|x1x2x3x4x5x6x7x8x9
X′2=x0|x3x4x5x6|x8x4x7x6x2x1x3x5x9
③依次刪除X′1和X′2中與交叉區相同的基因,得到最終的子串:
X″1=x0x7x6x2x1x3x4x5x8x9
X″2=x0x3x4x5x6x8x7x2x1x9
S2-5)交叉操作完成后,采用逆轉變異方法對染色體進行變異操作;同樣,以10個基因的染色體為例進行說明:如染色體(x0x1x2x3x4x5x6x7x8x9)在區間x2x3和區間x6x7處發生斷裂,斷裂片段又以反向順序插入,于是逆轉后的染色體變為(x0x1x2x6x5x4x3x7x8x9)。
S2-6)變異操作完成后,將種群中的個體按適應度從大到小排序,從大到小選擇N個適應度高的個體,作為下一次迭代的種群;迭代次數加1,并判斷是否達到設置的迭代次數,若達到則終止遺傳算法,否則,進入下一次遺傳算法的循環,直至迭代完成。
所述步驟S3中的最大最小蟻群算法在搜索最終測試路徑時,按照偽隨機比例規則搜索最終測試路徑的節點,具體地,螞蟻按照下面的公式搜索最終測試路徑的節點:
其中,q0∈(0,1)是常數,q∈(0,1)是隨機數,τij(t)表示t時刻節點v″i和v″j間的信息素,ηij(t)表示啟發信息,ηij(t)=1/dij,dij為數字微流控芯片災難性故障測試模型G″(V″,E″)中兩節點v″i和v″j間的距離,α和β分別表示影響信息素和啟發信息的相對強弱的兩個參數。
螞蟻搜索最終測試路徑節點的具體過程如下:
螞蟻在選擇下一節點時,先隨機生成q,若q≤q0,則選擇使[τil(t)]α[ηil(t)]β值最大的節點j否則按概率公式選擇下一個路由節點,按照公式計算每個節點被選擇的概率后,按照“輪盤賭”的方式選擇下一測試節點,即概率值越高被選擇的可能性越大。l∈allowedk表示節點l在可選的集合中,螞蟻選擇此節點后就從allowedk集合中刪除此節點,防止測試液滴的重復遍歷,提高測試效率。
本例中,最大最小蟻群算法的相關參數的優選設置方案如下:
螞蟻數量m=30,偽隨機比例規則中的q0=0.1,信息素啟發系數α=1.2,啟發因子系數β=3.0,信息素殘留系數ρ=0.92,收斂于最優解的概率Pbest=0.05,蟻群算法迭代次數設為1850。
步驟S3中最大最小蟻群算法的信息素更新策略為:只允許每次迭代后的最短測試路徑增加信息素,具體地,信息素按照下面的公式更新:
其中,ρ是信息素殘留系數,Δτij(t)表示路徑(i,j)上的信息素增量。f(Sbest)為本次最大最小蟻群算法迭代中最短測試路徑的長度Lls或當前全局最短測試路徑的長度Lgs。
所述f(Sbest)的具體設置方案為:在蟻群算法搜索測試路徑時,每次迭代后都采用本次迭代中最短測試路徑的長度Lls的值更新信息素,在固定的迭代次數選擇使用當前全局最短測試路徑的長度Lgs。本實施例中每迭代50次就使用一次前全局最短測試路徑的長度Lgs的值。
所述步驟S3中最大最小蟻群算法的信息素更新策略為:只允許每次迭代后的最短測試路徑增加信息素,具體地,信息素按照下面的公式更新:
其中,ρ是信息素殘留系數,Δτij(t)表示路徑(i,j)上的信息素增量。f(Sbest)為本次最大最小蟻群算法迭代中最短測試路徑的長度Lls或當前全局最短測試路徑的長度Lgs。
所述步驟S3中的最大最小蟻群算法的信息素上下界采用動態更新策略,具體地,信息素上下界更新公式如下:
其中,τmax(t)、τmin(t)為t時刻信息素的上下界,Lls為本次最大最小蟻群算法迭代后最短測試路徑的長度。
所述步驟S3中采用最大最小蟻群算法搜索最終測試路徑時,為了防止液滴之間的意外融合,測試液滴需要滿足靜態約束條件和動態約束條件,液滴之間的靜態約束條件和動態約束條件說明如下:如圖5所示,黑色實心圓表示液滴,“×”表示此單元此時刻t不能被測試液滴訪問,靜態約束條件是指液滴周圍直線相鄰和對角相鄰的單元上,同一時刻t不能同時存在其他液滴,即為了防止液滴間的意外融合,液滴之間需要保持一定的距離,用公式表示如下:
或
動態約束條件是指液滴下一時刻移動的位置不能與其他液滴相鄰,用公式可表示為:
根據實驗液滴的移動路徑和約束條件可以確定任意時刻t不能被測試液滴訪問的單元的集合,記為禁忌表tab(t)。在利用最大最小蟻群算法搜索測試路徑中的節點時,若某時刻t選擇的路由節點j處于禁忌表tab(t)中,則表示此節點當前不可訪問,查詢此節點被禁止的時間,設為等待時間twait;按照偽隨機比例規則重新搜索新的節點x,將當前節點i到原選擇節點j的距離權值加上等待時間twait的權值與當前節點i到新節點x的距離權值作比較,若到達新節點x距離權值較小,則測試液滴向新節點x移動,否則測試液滴在當前節點i等待原選節點j被激活,選擇節點j。
步驟S3中采用最大最小蟻群算法搜索最終測試路徑時,當蟻群算法迭代次數到達設定值后,輸出求得最終測試路徑。本實施例中最大最小蟻群算法迭代1850次后,輸出求得的最終測試路徑,并根據求得的最終測試路徑計算測試花費的單位時間,測試路徑越長則測試花費的單位時間越多,測試路徑越短則測試花費的單位時間越少。測試花費的單位時間越少,說明測試效率越高。其中,單位時間為測試液滴從一個單元移動到相鄰單元花費的時間,本實施例中,如圖1所示的多元生化實驗的數字微流控芯片的單位時間具體為62.5ms。
按照上述步驟對圖1所示的數字微流控芯片進行災難性故障測試仿真,測試算法在Visual studio 2012環境下采用C++編程實現,得到的測試方法收斂示意圖如圖4所示,圖4的橫坐標為迭代次數,縱坐標為單位時間;圖5中縱坐標為單位時間,橫坐標為不同的測試方法;由圖5可知,本實施例的測試算法的測試花費時間明顯優于歐拉回路法,比蟻群算法的測試花費時間僅多1個單位時間。但是,單一的蟻群算法一般在迭代1350次左右收斂,由圖4可知,本實施例的方法在950次左右算法收斂,相比單一的蟻群算法收斂性提了29%,方法的收斂性更好,在保證了測試花費時間較低的情況下,能夠快速地求得較優的測試路徑。
由于漢密爾頓回路測試法、分區子陣列合并調度測試法無法檢測出相鄰電極短路故障,并行測試和自建自測試法只能用于規則陣列的芯片測試,這些測試方法缺少全面性、兼容性,本實施例的測試方法不與這些測試方法作比較。
- 還沒有人留言評論。精彩留言會獲得點贊!