本發明涉及一種橡膠O形圈有限元建模方法，特別涉及一種用于結構動力學仿真的橡膠O形圈有限元建模方法。

背景技術：

O形圈是軸孔配合結構最常用的密封方式之一，由于其質量與剛度遠小于軸結構和孔結構，因此在進行軸孔配合結構整體動力學仿真分析時，O形圈結構通常被忽略。但是，當軸結構和孔結構之間的連接剛度與O形圈的剛度處于同一個數量級或者軸結構和孔結構之間的連接剛度完全由O形圈提供時，忽略O形圈結構，將導致整體結構動力學模型出現較大誤差。

ANSYS等大型通用非線性有限元程序通常采用Mooney-Rivlin模型分析和計算橡膠的力學性能.

文獻“液壓伺服作動器O形密封圈實驗研究與有限元分析[D],哈爾濱工業大學,2011,P31-47”公開了一種橡膠O形圈有限元建模方法，該方法在建立O形橡膠密封圈有限元模型過程中，選用幾個參數表示的應變能密度函數來描述超彈性體不可壓縮材料特性。而為了確定Mooney-Rivlin模型參數，文獻通過對丁腈橡材料的膠啞鈴狀試件進行等雙軸拉伸實驗、單軸拉伸實驗和剪切實驗，根據實驗測得的應力應變數據，利用MATLAB軟件線性回歸和ANSYS軟件的計算，求出了試件的Mooney-Rivlin常數，從而為O形橡膠密封圈有限元建模提供材料特性參數。由于橡膠材料的非線性、不可壓縮性和大變形性，文獻中用試驗方法確定橡膠材料力學性能常數的過程繁雜，且試驗采用的膠啞鈴狀模型試件與O形圈結構不一致，其力學性能參數也有偏差，試驗件的制備也耗時費力。而且，該種方法以靜力學試驗確定的材料特性參數多運用于研究材料失效、受壓下的變形和可靠性等靜密封及微動密封特性分析，對于通過O形圈密封連接軸和孔的整體結構系統的動力學仿真建模，該種方法確定的力學性能參數未必適用。

技術實現要素：

為了克服現有橡膠O形圈有限元建模方法復雜的不足。本發明提供一種用于結構動力學仿真的橡膠O形圈有限元建模方法。該方法對軸結構、孔結構和O形圈組成的系統進行結構簡化，建立其有限元模型；然后對系統進行自由邊界條件下的模態試驗，獲得固有頻率、振型等模態參數；以模態仿真計算結果與模態試驗結果的誤差最小為目標函數，采用優化算法確定O形圈的彈性模量E，從而獲得具有較高精度的O形圈有限元模型。該方法可以獲取具有較高仿真精度的軸孔配合結構的動力學仿真模型，進而獲得高精度的動力學仿真結果，方法簡單。

本發明解決其技術問題所采用的技術方案是：一種用于結構動力學仿真的橡膠O形圈有限元建模方法，其特點是包括以下步驟：

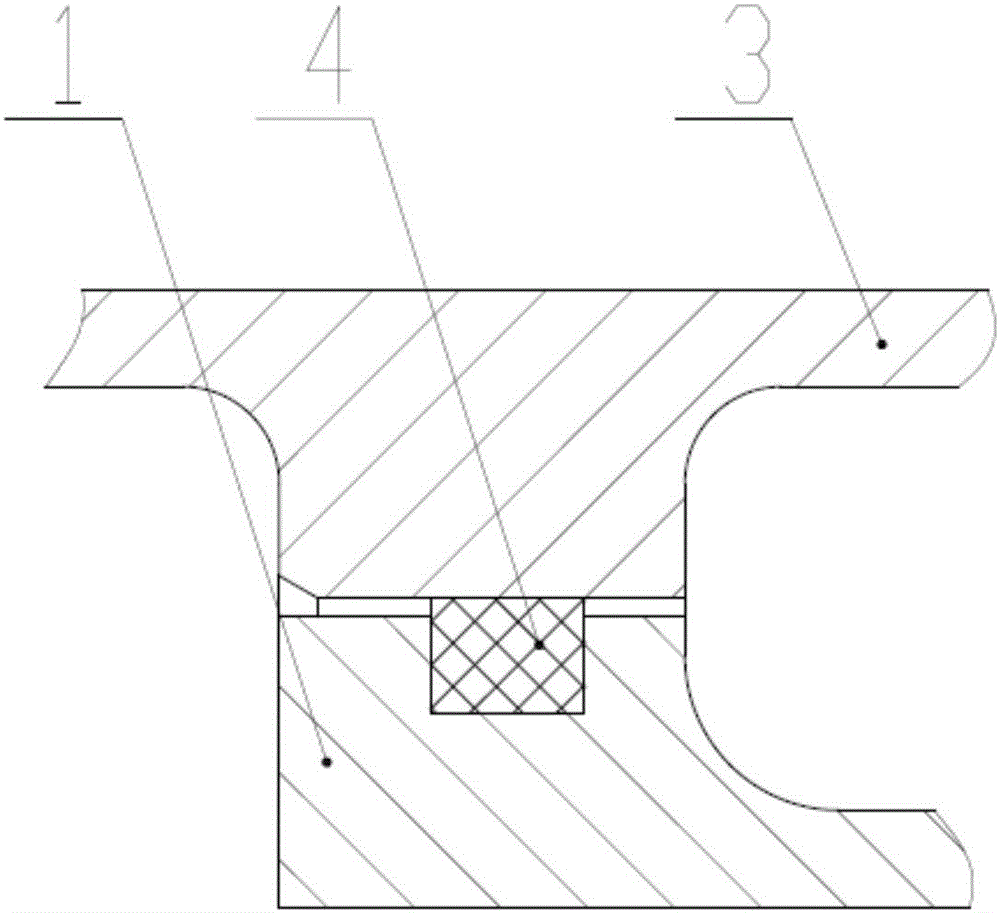
步驟一、O形圈2結構等效。

為了便于建立O形圈2的有限元模型，設定O形圈2裝配后的理想狀態條件為：

a)O形圈2裝入孔結構3與軸結構1構成的O形圈槽后，填滿O形圈槽；

b)O形圈2外表面與孔結構3無相對運動；

c)O形圈2內表面與軸結構1無相對運動。

步驟二、建立系統的有限元模型。

軸結構1和孔結構3按實際結構尺寸進行建模，其彈性模量E、泊松比ν和密度ρ參數按結構材料的物理參數設置；O形圈2按照理想狀態條件a)進行建模，其泊松比ν和密度ρ按O形圈2材料的物理參數設置，彈性模量E為待定變量；O形圈2與軸結構1和孔結構3之間的連接關系按照理想狀態條件b)和c)進行處理。

步驟三、確定模態參數。

以軸結構1、孔結構3和O形圈2組成的系統為對象，在自由邊界條件下，對系統進行模態試驗，獲取自由邊界條件下系統的固有頻率、振型這些模態參數。

步驟四、確定等效O形圈4等效彈性模量E_x。

采用優化算法求解等效O形圈4的等效彈性模量E_x。定義等效O形圈4的等效彈性模量E_x作為設計變量，E_x的取值范圍為0.01E～10E，E為材料的彈性模量；定義模態仿真計算結果與模態試驗結果的誤差最小為目標函數f(x)，即

式中，i表示固有頻率和模態振型的階次；表示第i階固有頻率仿真計算值和試驗值誤差的絕對值；MAC_i表示第i階模態振型仿真計算值和試驗值的相關性；α_i和β_i分別表示第i階固有頻率的誤差和MAC值殘差的加權系數，和MAC_i均為等效O形圈4等效彈性模量E_x的函數。

所述α_i和β_i取值均為1。

本發明的有益效果是：該方法對軸結構、孔結構和O形圈組成的系統進行結構簡化，建立其有限元模型；然后對系統進行自由邊界條件下的模態試驗，獲得固有頻率、振型等模態參數；以模態仿真計算結果與模態試驗結果的誤差最小為目標函數，采用優化算法確定O形圈的彈性模量E，從而獲得具有較高精度的O形圈有限元模型。該方法可以獲取具有較高仿真精度的軸孔配合結構的動力學仿真模型，進而獲得高精度的動力學仿真結果，動力學仿真結果與試驗結果誤差保持在10％以內，方法簡單。

下面結合附圖和具體實施方式對本發明作詳細說明。

附圖說明

圖1是本發明方法所涉及的軸孔配合結構的O形圈結構圖。

圖2是等效后的O形圈結構圖。

圖中，1-軸結構，2-O形圈，3-孔結構，4-等效O形圈。

具體實施方式

參照圖1-2。本發明以軸孔配合結構的O形圈為研究對象，用于結構動力學仿真的橡膠O形圈有限元建模方法具體步驟如下：

步驟一、O形圈2結構等效。

為了便于建立O形圈2的有限元模型，設定O形圈2裝配后的理想狀態條件為：

a)O形圈2裝入孔結構3與軸結構1構成的O形圈槽后，填滿O形圈槽；

b)O形圈2外表面與孔結構3無相對運動；

c)O形圈2內表面與軸結構1無相對運動。

步驟二、建立系統的有限元模型。

軸結構1和孔結構3按實際結構尺寸進行建模，其彈性模量E、泊松比ν和密度ρ等參數按結構材料的物理參數設置；O形圈2按照理想狀態條件a)進行建模，其泊松比ν和密度ρ按O形圈2材料的物理參數設置，彈性模量E為待定變量；O形圈2與軸結構1和孔結構3之間的連接關系按照理想狀態條件b)和c)進行處理。

步驟三、確定模態參數。

以軸結構1、孔結構3和O形圈2組成的系統為對象，在自由邊界條件下，對系統進行模態試驗，獲取自由邊界條件下系統的固有頻率、振型等模態參數。

步驟四、確定等效O形圈4等效彈性模量E_x。

采用優化算法求解等效O形圈4的等效彈性模量E_x。定義等效O形圈4的等效彈性模量E_x作為設計變量，其取值范圍定義為0.01E～10E(E為材料的彈性模量)；定義模態仿真計算結果與模態試驗結果的誤差最小為目標函數f(x)，即

式中，i表示固有頻率和模態振型的階次；表示第i階固有頻率仿真計算值和試驗值誤差的絕對值；MAC_i表示第i階模態振型仿真計算值和試驗值得相關性；α_i和β_i分別表示第i階固有頻率的誤差和MAC值殘差的加權系數，通常情況下均取1。和MAC_i均為等效O形圈4等效彈性模量E_x的函數。