本發(fā)明涉及了一種金屬微波器件分析計(jì)算方法，尤其是涉及了一種電磁器件分析中電磁-熱-應(yīng)力三場耦合的去耦合計(jì)算方法。

背景技術(shù)：

所謂多物理場耦合，指在一個(gè)系統(tǒng)中，多個(gè)物理場交織在一起，互相影響，互相作用而彼此影響的物理現(xiàn)象，這種現(xiàn)象在客觀世界和工程實(shí)際中廣泛存在，只要多個(gè)物理場存在且各物理場之間發(fā)生了能量交換，必然隨之會(huì)產(chǎn)生多物理場耦合系統(tǒng)。各種物理場現(xiàn)象都可以用偏微分方程來描述，如熱、電、力。多物理場的本質(zhì)是偏微分方程組。

金屬微波器件是非常典型的、具有強(qiáng)烈耦合度的多物理場環(huán)境，包括電磁場、溫度場、力場的相互耦合。由于很多因素同時(shí)起作用，必須給出一種可以同時(shí)處理這些因素作用的多物理場聯(lián)合分析方法。

描述金屬微波器件涉及電磁、熱、力多種物理現(xiàn)象的組合，而這些現(xiàn)象都基于特定的物理規(guī)律，這些物理規(guī)律可借助于偏微分方程得到精確描述和分析。故解決多物理場耦合的基礎(chǔ)是建立它們的數(shù)學(xué)模型，這需要充分了解各物理場的基本理論，列出其數(shù)學(xué)模型(偏微分方程組)，多物理場分析意味著求解多維度的偏微分方程組。系統(tǒng)性地討論它們之間的場耦合關(guān)系，得到偏微分方程體系，建立電-熱-應(yīng)力約束條件下的典型空間金屬微波器件模型。

技術(shù)實(shí)現(xiàn)要素：

為了簡化電磁-熱-應(yīng)力三場耦合計(jì)算的復(fù)雜度，本發(fā)明的目的在于提供了一種電磁器件分析中電磁-熱-應(yīng)力三場耦合的去耦合計(jì)算方法。

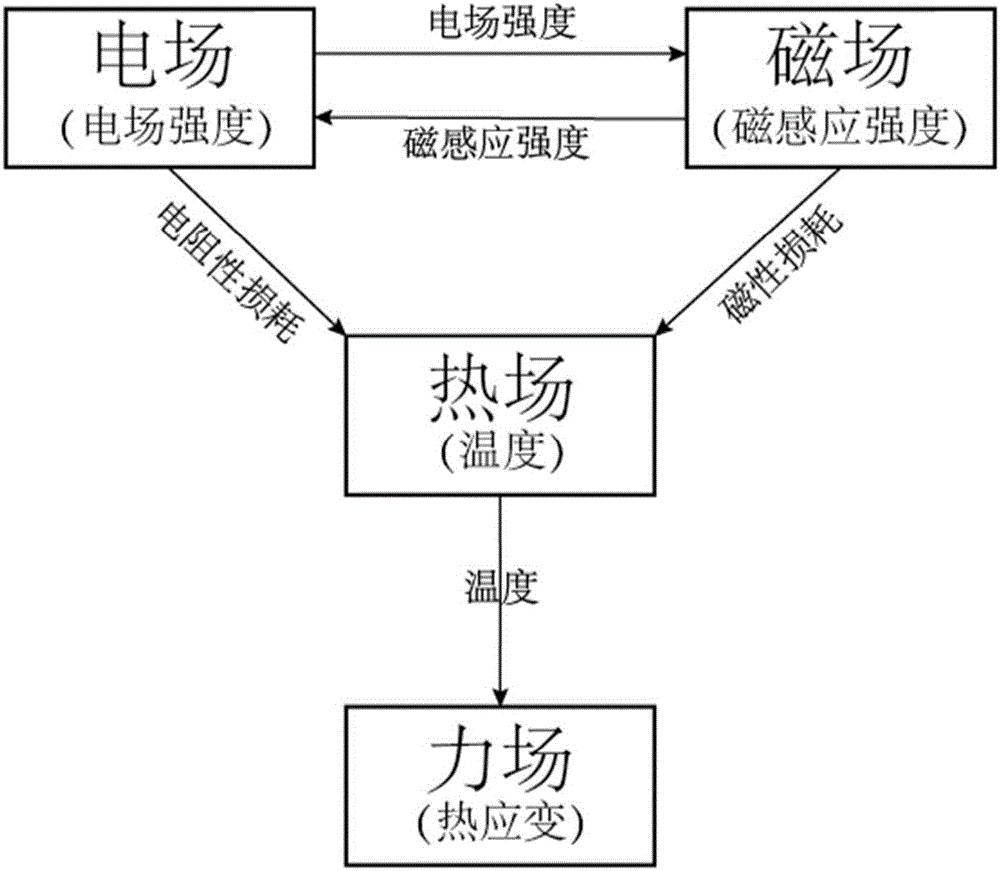
為了達(dá)到上述目的，本發(fā)明采用的技術(shù)方案是如圖1所示：根據(jù)電磁波傳播原理與阻抗邊界條件建立電磁波在金屬微波器件內(nèi)壁的微波電磁損耗模型，通過微波電磁損耗模型將電磁場和力場之間去耦合，使得電磁場通過溫度場間接與力場耦合，進(jìn)而對力場分布計(jì)算。

電磁-熱-力場之間存在著耦合作用，從原理上來說，由于電磁損耗，微波器件中大功率微波的傳播會(huì)在微波器件內(nèi)部產(chǎn)生熱損耗Q(包括電阻性損耗Q_rh與磁性損耗Q_ml)。電阻性損耗可用介質(zhì)的損耗角正切tanδ或介電常數(shù)的虛部ε來表示，與材料的電阻率有關(guān)，電阻率越大，阻性損耗越小。磁性損耗主要存在于磁性材料中，與復(fù)磁導(dǎo)率的虛部μ成正比。電磁損耗熱效應(yīng)產(chǎn)生的熱成為溫度場的場源，求解熱傳遞方程可確定溫度場的分布。而溫度場對結(jié)構(gòu)的作用表現(xiàn)為溫度差導(dǎo)致物體的膨脹或縮小，從而產(chǎn)生熱應(yīng)變?chǔ)?sub>inel。作為力場的場源，通過求解線彈性力學(xué)方程組可得到應(yīng)變、位移與應(yīng)力的分布。現(xiàn)有技術(shù)中，電磁場、溫度場和力場三個(gè)物理場通過彼此提供物理場場源的方式進(jìn)行耦合。而本發(fā)明使得電磁場和力場之間去耦合，電磁場的電場和磁場與溫度場耦合，溫度場與力場耦合，電場和磁場分別與力場之間不耦合。

所述的平面波入射到金屬微波器件，在金屬微波器件的內(nèi)部形成電磁場分布并產(chǎn)生熱量，先計(jì)算獲得金屬內(nèi)壁產(chǎn)生的熱損耗分布，熱損耗包括電阻性損耗和磁性損耗，將熱損耗分布作為熱源以賦值到熱應(yīng)力場的方式進(jìn)行求解得到溫度場分布，根據(jù)溫度場分布計(jì)算獲得熱應(yīng)變分布，獲得去耦合計(jì)算結(jié)果。

本發(fā)明將三個(gè)物理場分為兩個(gè)步驟電磁-熱、熱-應(yīng)力進(jìn)行分步計(jì)算，具體是在所述平面波入射到金屬微波器件采用以下方式計(jì)算獲得去耦合計(jì)算結(jié)果：

第一，先通過電場形式下具有附加邊界條件的波動(dòng)方程獲得金屬微波器件內(nèi)的電場分布，接著利用麥克斯韋方程組以及金屬微波器件與其外部環(huán)境內(nèi)在的本構(gòu)關(guān)系計(jì)算出電位移、磁感應(yīng)強(qiáng)度、磁場強(qiáng)度和自由電流密度物理量，從而獲得電磁場分布情況；

第二，采用以下公式計(jì)算獲得電阻性損耗Q_rh與磁性損耗Q_ml：

其中，Re表示實(shí)部，j表示虛數(shù)單位，ω表示角頻率，和分別為磁感應(yīng)強(qiáng)度矢量和磁場強(qiáng)度矢量，為電場強(qiáng)度矢量，為自由電流密度矢量；電阻性損耗可用介質(zhì)的損耗角正切tanδ或介電常數(shù)的虛部ε來表示，與材料的電阻率有關(guān)，電阻率越大，阻性損耗越小。磁性損耗主要存在于磁性材料中，與復(fù)磁導(dǎo)率的虛部μ成正比。

將電阻性損耗Q_rh與磁性損耗Q_ml相加作為熱源的大小，代入以下熱傳導(dǎo)方程求解獲得問題，進(jìn)而得到溫度場分布：

其中，ρ為密度，C_ρ為恒壓下的熱容，為傳導(dǎo)熱通量，k為熱導(dǎo)率，Q為熱損耗；

第三，溫度的變化引起熱應(yīng)變，采用以下公式表示的線彈性力學(xué)方程計(jì)算得到熱應(yīng)變?chǔ)?sub>inel，進(jìn)而得到熱應(yīng)變分布：

ε_inel＝α(T-T_ref)

其中，α為熱膨脹系數(shù)，T_ref表示金屬微波器件的原始溫度。

所述的微波電磁損耗模型適用于金屬微波器件，所述金屬微波器件包括波導(dǎo)法蘭、同軸連接器等。

本發(fā)明的溫度場還會(huì)影響微波電磁損耗模型的材料系數(shù)。一些材料參數(shù)，諸如材料密度ρ、熱容Cp、泊松比μ等對溫度是不敏感的，在溫度變化時(shí)可將它們看成常數(shù)，通常取常溫時(shí)的值。其它的物理參數(shù)包括電導(dǎo)率σ、熱導(dǎo)率k、楊氏模量E以及熱膨脹系數(shù)α是溫度的函數(shù)。

本發(fā)明的有益效果是：

本發(fā)明能夠分析電磁波在金屬微波器件中傳播時(shí)，在腔體表面產(chǎn)生損耗，進(jìn)而形成熱效應(yīng)，以致器件在熱應(yīng)力作用下形變的情況，簡便而準(zhǔn)確地計(jì)算出溫度的變化以及隨之產(chǎn)生的應(yīng)力和形變。

附圖說明

圖1為本發(fā)明實(shí)施例方法的原理示意圖。

圖2是本發(fā)明實(shí)施例提供的微波電磁損耗模型的示意圖。

圖3是本發(fā)明實(shí)施例電磁波在器件內(nèi)部傳播的電場強(qiáng)度分布圖。

圖4是本發(fā)明實(shí)施例電磁波在器件表面的熱損耗分布圖。

圖5是本發(fā)明實(shí)施例電磁波在器件內(nèi)部傳播引起的應(yīng)力分布圖。

具體實(shí)施方式

下面結(jié)合本發(fā)明實(shí)施例中的附圖，詳細(xì)描述本發(fā)明的實(shí)施過程。

本發(fā)明的實(shí)施例如下：

如圖2所示為微波在器件表面的損耗模型，實(shí)施例的平面波沿金屬微波器件長度方向入射到金屬微波器件的內(nèi)腔中，損耗區(qū)域?yàn)槲⒉ㄆ骷?nèi)表面。主要分成三個(gè)過程：

第一個(gè)過程，平面波入射微波器件在其內(nèi)部形成電磁場分布。假設(shè)由器件端口向其內(nèi)部入射平面波，根據(jù)電磁波自由空間傳播得到在微波器件內(nèi)部的電磁場分布，即麥克斯韋方程組：

電流連續(xù)性定理

磁通連續(xù)性定理

高斯定理

法拉第定理

廣義安培定理

其中，表示拉普拉斯算子，t表示時(shí)間，和分別為電場強(qiáng)度矢量和電位移矢量，和分別為磁感應(yīng)強(qiáng)度矢量和磁場強(qiáng)度矢量，ρ_v和分別為自由電荷密度和自由電流密度矢量；

另外采用以下由介質(zhì)特性決定的三個(gè)方程，即本構(gòu)關(guān)系，聯(lián)立計(jì)算得到電位移、磁感應(yīng)強(qiáng)度和自由電流密度，并同時(shí)相應(yīng)計(jì)算獲得磁場強(qiáng)度：

其中，為傳導(dǎo)電流密度，為真空中或氣體中電流密度，ε為介質(zhì)介電常數(shù)，μ為介質(zhì)磁導(dǎo)率，σ為導(dǎo)體電導(dǎo)率，ρ_v為真空或氣體中荷電粒子的密度，為真空或氣體中荷電粒子的速度。

第二個(gè)過程，計(jì)算熱場。由于不是完純導(dǎo)體，微波器件內(nèi)表面也存在一定的電磁場分布，主要存在于趨膚深度的厚度內(nèi)，電流集中在導(dǎo)體表面，稱為表面電流，可由麥克斯韋方程以及阻抗邊界條件求得，阻抗邊界條件采用以下公式表示：

將其代入電阻性損耗公式即可求得電磁波傳播在微波器件內(nèi)部產(chǎn)生的熱損耗。

在固體中，實(shí)施例采用的熱傳遞方程表示為如下公式：

其中，ρ為密度(kg/m³)，T表示溫度，C_ρ為恒壓下的熱容(J/(kg·K))，為傳導(dǎo)熱通量(W/m²)，k為熱導(dǎo)率(W/(m·K))，Q為熱損耗(W/m³)。

熱傳遞方程包括兩種基本的邊界條件：指定的溫度和指定的熱通量。

第三個(gè)過程，用已經(jīng)計(jì)算出的熱損耗為源，求解應(yīng)力場。

金屬微波器件滿足線彈性材料的條件，實(shí)施例的線彈性材料模型用如下所示的方程組來描述，可計(jì)算得到熱應(yīng)變?chǔ)?sub>inel：

s-s₀＝C:(ε-ε₀-ε_inel)

ε_inel＝α(T-T_ref)

其中，s表示應(yīng)力，表示位置，α為熱膨脹系數(shù)，T_ref為應(yīng)變參考溫度，s₀為初始應(yīng)力，ε為應(yīng)變張量，ε₀為初始應(yīng)變，C為彈性張量，:為張量積。上述三個(gè)公式分別為應(yīng)變-位移關(guān)系式、Duhamel-Hooke定律以及應(yīng)力張量與應(yīng)變張量及溫度的關(guān)系。

在金屬微波器件的線彈性材料中，由于材料的對稱性，上述應(yīng)力張量ε寫成以下的矩陣形式：

其中，ε_x、ε_y和ε_z屬于正應(yīng)變，ε_xy、ε_yz和ε_xz屬于剪切應(yīng)變，分別表示張量ε的九個(gè)分量。

同理，應(yīng)力張量s和熱膨脹張量α也寫成類似的矩陣形式，將張量用九個(gè)分量表示：

本發(fā)明具體實(shí)例是以長300mm，寬123.22mm，高68.61mm，波導(dǎo)壁厚度7mm的直波導(dǎo)為例，在其一端輸入25W，2.4GHz的平面波，電場分布在x、z方向上無變化，在y方向上是余弦函數(shù)(附圖3)，同樣的，熱損耗在x、z方向上不變，y方向?yàn)閏os²分布(附圖4)，具體熱損耗函數(shù)為：

Q＝[0.347cos(πy/109.22)]^2+0.11

以熱損耗Q為源，在熱應(yīng)力場中可以求得溫度和應(yīng)力的變化，波導(dǎo)整體上升了約0.00007K，應(yīng)力分布有兩種情況(附圖5)，波導(dǎo)內(nèi)部分布均勻，在110MPa左右，端口處應(yīng)力主要分布在四個(gè)角，最大處約為450MPa。

本發(fā)明技術(shù)領(lǐng)域涉及的計(jì)算涉及大量偏微分方程，較為復(fù)雜，多為軟件仿真使用。由于電磁與應(yīng)力場的耦合影響極小，卻又占據(jù)計(jì)算大量內(nèi)存，在工程上完全可以忽略，因此通過本發(fā)明方法將原來長達(dá)數(shù)個(gè)小時(shí)的計(jì)算簡化到半個(gè)小時(shí)以內(nèi)，大大提高了效率，精簡了過程，也可減小多步計(jì)算的誤差。

以上所述，僅為本發(fā)明的具體實(shí)施方式，但本發(fā)明的保護(hù)范圍并不局限于此，任何熟悉本技術(shù)領(lǐng)域的技術(shù)人員在本發(fā)明披露的技術(shù)范圍內(nèi)，可輕易想到的變化或者替換，都應(yīng)涵蓋在本發(fā)明的保護(hù)范圍之內(nèi)。因此，本發(fā)明的保護(hù)范圍應(yīng)該以權(quán)力要求書的保護(hù)范圍為準(zhǔn)。