本發(fā)明涉及電機控制領域，具體涉及一種永磁同步電機中低速轉子位置估算方法。
背景技術：
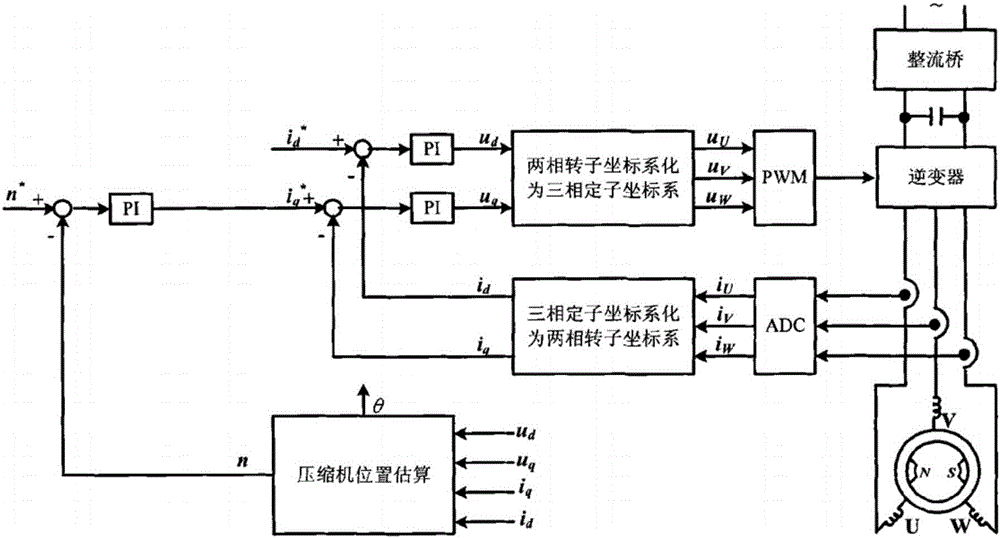
：隨著世界能源形勢的口益嚴峻，世界各國對能源及節(jié)能技術越來越重視。我國政府對能源的重視也提升到了一個前所未有的高度，尤其在國家"十一五計劃"中就重點提到了節(jié)能的要求。直流變頻空調(diào)由于節(jié)能效果明顯而日益受到市場的廣泛關注。直流變頻空調(diào)一般分方波變頻(120度矩形波)和正弦波變頻(180度正弦波)，其中正弦波變頻控制技術是2002年才剛剛投入空調(diào)市場的最新變頻技術，與方波變頻技術相比具有效率高、控制壓縮機運行平穩(wěn)、噪音低的優(yōu)勢，更是未來變頻技術的發(fā)展方向。正弦波變頻控制技術中需要時刻知道壓縮機轉子的位置，傳統(tǒng)的方案是在壓縮機上裝霍爾元件來檢測轉子的位置，但是由于壓縮機是個封閉的系統(tǒng)，霍爾元件容易受到溫度、濕度和震動等條件的限制，使其可靠性大大降低，同時也增加了電機的成本。為了克服上述缺點，就需要采用一種算法來間接地實現(xiàn)電機位置的檢測。現(xiàn)有的技術(電氣學會論文集D117卷1號1997年98-104或者CN1264212A里有引用)是根據(jù)期望坐標系下的電流與實際坐標系下的電流差來估算壓縮機的反電動勢，進而得知壓縮機轉子的位置。技術實現(xiàn)要素：本發(fā)明提供一種電機中低速轉子位置估算方法，目的是通過該估算算法間接地檢測電機轉子的位置，用以實現(xiàn)例如空調(diào)用正弦波變頻控制。本發(fā)明的目的是由以下技術方案實現(xiàn)的：一種電機中低速轉子位置估算方法，其特征在于，包括如下步驟：(1)建立實際旋轉坐標系下定子電壓方程；(2)建立與實際旋轉坐標系夾角Δθ的期望旋轉坐標系下的定子電壓方程；(3)計算期望旋轉坐標系下的電壓與實際旋轉坐標系下的電壓之差；(4)根據(jù)期望旋轉坐標系下的電壓與實際旋轉坐標系下的電壓之差估算電機反電動勢；(5)根據(jù)估算的電機反電動勢進而估算出轉子的速度。一種電機驅(qū)動控制方法，包括如下步驟：(I)首先讀取電機三相電流A/D采樣數(shù)據(jù)；(II)將的三相電流A/D采樣數(shù)據(jù)轉換為兩相旋轉坐標系下的電流數(shù)據(jù)；(III)電機位置估算；(IV)電壓矢量控制；(V)生成PWM信號給逆變器；本發(fā)明與現(xiàn)有技術相比較，具有估算公式簡單，引入?yún)?shù)少的特點，從而減小了電機參數(shù)對估算反電動勢以及速度的影響，提高了速度估算的準確性以及系統(tǒng)的穩(wěn)定性。附圖說明圖1為期望坐標軸與實際坐標軸關系圖；圖2為空調(diào)系統(tǒng)正弦波矢量控制系統(tǒng)框圖：圖3為空調(diào)系正弦波矢量控制流程圖；圖4a現(xiàn)有技術的低頻段有死區(qū)時間的電機的電流；圖4b采用本發(fā)明方法的低頻段有死區(qū)時間的電機的電流。具體實施方式實施例一請參見圖1，無位置傳感器永磁同步電機由定子繞組和永磁體轉子組成，其中U、V、W軸為電機的各相繞組的中心線，d、q軸為實際轉子旋轉坐標系下的軸線，γ、δ軸為期望旋轉坐標系下的軸線,d軸與U軸之間的夾角為電機轉角θ，γ軸與U軸之間的夾角為估算的電機轉角θM，γ軸與d軸之間的夾角為Δθ。當Δθ很小時，期望旋轉坐標軸與實際轉子坐標軸重合，此時期望的速度與實際速度相一致，這樣達到了轉子位置估算的目的。轉子在實際坐標軸d、q下的電機方程為：ud＝Rid+pLdid-Lqiqωuq＝Riq+pLqiq+Ldidω+e其中，ud、uq分別為定子電壓d、q軸分量；id、iq分別為定子電流d、q軸的分量；Ld、Lq分別為d、q軸電感；R為定子相電阻；e為電機反電動勢；p為微分系數(shù)；ω為轉子電轉速。當期望坐標軸γ、δ與實際坐標軸d、q之間夾角為Δθ時，期望坐標系下的電機方程如下：uγ＝Riγ+pLdiγ-Lqiδω-esinΔθuδ＝Riδ+pLqiδ+Ldiγω+ecosΔθ(1)其中，uγ、uδ別為定子電壓γ、δ軸分量；iγ、iδ分別為定子電流γ、δ軸分量。將上述方程離散化，令采樣時間為T可得：uγ(n)=Riγ(n)+LdTiγ(n)-LdTiγ(n-1)-θ·(n)Lqiδ(n)-esinΔθuδ(n)=Riδ(n)+LqTiδ(n)-LqTiδ(n-1)+θ·(n)Ldiγ(n)+ecosΔθ---(2)]]>其中，θ為估算轉子位置；iδ(n)、iγ(n)分別為定子電流γ、δ軸分量第n采樣周期值；iδ(n-1)、iγ(n－1)分別為定子電流γ、δ軸分量第n-1采樣周期值；為估算轉子位置的微分。而我們期望Δθ＝0，這樣期望的速度就與實際坐標系下的速度基本一致，在此時的電機方程如下：uMγ(n)=Riγ(n)+LdTiγ(n)-LdTiγ(n-1)-θ·(n)Lqiδ(n)uMδ(n)=Riδ(n)+LqTiδ(n)-LqTiδ(n-1)+θ·(n)Ldiγ(n)+e(M)(n-1)---(3)]]>其中，uMδ(n)、uMγ(n)分別為模型定子電壓γ、δ軸分量；eM(n-1)為期望旋轉坐標系上一次反電動勢。將上述公式(2)與公式(3)相減，得到：uMγ(n)uMδ(n)-uγ(n)uδ(n)=Δuγ(n)Δuδ(n)=esinΔθeM(n-1)-ecosΔθ≈]]>eΔθ-Δe---(4)]]>其中，uγ(n)、uδ(n)分別為期望旋轉坐標系電壓γ、δ軸分量與實際旋轉坐標系電壓d、q軸之差；Δe為反電動勢估算誤差。公式(4)中Δe＝e-eM(n-1),在這里Δθ接近零，所以可以得到：eM(n)＝eM(n-1)-KeΔuδ(n)(5)其中，Ke為反電動勢系數(shù),eM(n)為本次反電動勢；Δuδ(n)為δ角下的本次電壓差。從電壓之差公式(4)中，可以得到如下轉角公式：θM(n)=θM(n-1)+TKEeM(n)+Kθsign{θ·M0(n-1)}Δuγ(n)---(6)]]>其中，KE為反電勢系數(shù)；其中為轉子位置估算常數(shù)；θM(n)為本次轉子位置角；θM(n-1)為上一次轉子位置角；T為采樣時間；Δuγ(n)為γ角下的本次電壓差；為本次轉子位置角的微分；為上一次轉子位置角的微分。根據(jù)公式(6)可以得到轉速公式：θ·M(n)=1T{θM(n)-θM(n-1)}=eM(n)Ke+Δθ·M(n)---(7)]]>Δθ·M(n)=KθTsign{θ·M0(n-1)}Δuγ(n)---(8)]]>其中，為估算轉子位置誤差。由于采用周期較短，誤差被放大，所以公式(7)、(8)需要一階低通濾波，得到：θ·M0(n)=eM(n)Ke+Δθ·M0(n)---(9)]]>Δθ·M0(n)=Δθ·M0(n-1)+K{Δθ·M0(n)-Δθ·M0(n-1)}---(10)]]>其中，為的一階低通濾波值，K為比例系數(shù)。根據(jù)上述十個公式就可以實現(xiàn)壓縮機轉子位置的估算。其中，本發(fā)明中公式(4)是計算期望旋轉坐標系下的電壓與實際旋轉坐標系下的電壓之差，相比較現(xiàn)有技術計算電流差的公式：Δiγ(n)Δiδ(n)≈TLdeΔθ-TLqΔe]]>其中，Δiγ(n)、Δiδ(n)分別為模型電機定子電流γ、δ軸分量與實際電流之差，該公式(4)減小了電機參數(shù)對估算反電動勢以及速度的影響(在高溫高壓情況下電機的參數(shù)會發(fā)生變化)，提高了速度估算的準確性以及系統(tǒng)的穩(wěn)定性。此外在電機低頻段,由于死區(qū)時間的存在，導致壓縮機生電流產(chǎn)生畸變，與現(xiàn)有技術相比，本發(fā)明的電流波形更好，結合圖4a及圖4b。下面將上述電機轉子位置估算方法應用于空調(diào)的壓縮機控制中，圖2所示為變頻空調(diào)正弦波系統(tǒng)控制框圖，其程序流程圖如圖3所示。一種電機驅(qū)動控制方法，包括如下步驟：(I)首先讀取電機三相電流A/D采樣數(shù)據(jù)；(II)將三相電流A/D采樣數(shù)據(jù)轉換為兩相旋轉坐標系下的電流數(shù)據(jù)；(III)電機位置估算，具體地，根據(jù)公式(1)到(10)采用期望坐標系下的電壓與轉子旋轉坐標系下的電壓差估算壓縮機反電動勢，進而估算出壓縮機的電機速度n；(IV)電壓矢量控制；(V)生成PWM信號給逆變器；實施例二實施例二與實施例一的區(qū)別在于，在位置估算模塊中采用PI調(diào)節(jié)器來估算反電動勢，公式(5)、公式(6)與實施例一不同，如下：由公式(4)可以看出，反電動勢Δe與Δuδ成正比，采用PI調(diào)節(jié)器來估算反電動勢，公式如下：eM(n)＝－KpeMΔuδ(n)+eMX(n)eMX(n)＝-KieMΔuδ(n)+eMX(n-1)(11)其中KpeM為反電勢PI調(diào)節(jié)器比例系數(shù)；KieM為反電勢PI調(diào)節(jié)器積分系數(shù)；eMX(n)為本次電勢PI調(diào)節(jié)器積分分量；eMX(n-1)為上一次電勢PI調(diào)節(jié)器積分分量；eM(n)為本次反電動勢；Δuδ(n)為δ角下的本次電壓差。從4式中我們可以看出來，反電動勢e在一個采樣周期內(nèi)變化不大，可以認為不變，因而Δθ與Δuγ接近正比，在此也采用PI調(diào)節(jié)器來估算轉角θ，可以得到如下的轉角方程：θM(n)=Kpθsgn(θ·M(n-1))Δiγ(n)+θMX(n)θMX(n)=θMX(n-1)+Kiθsgn(θ·M(n-1))Δiγ(n)+eM(n)T/KE---(12)]]>其中，θM(n)為本次轉子位置角；θM(n-1)為上一次轉子位置角；Kpθ為估算轉角PI調(diào)節(jié)器比例系數(shù)；Kiθ為估算轉角PI調(diào)節(jié)器積分系數(shù)；θMX(n)為估算轉角PI調(diào)節(jié)器積分分量；θMX(n-1)為上一次估算轉角PI調(diào)節(jié)器積分分量；θM(n)為本次補償轉角的積分分量；為上一次補償角的微分常量；T為采樣時間；KE為轉矩比例系數(shù)；為Δiγ(n)、Δiδ(n)分別為模型電機定子電流γ、δ軸分量與實際電流之差。當前第1頁1 2 3