本發明涉及開關磁阻電機技術領域，具體為一種無軸承的開關磁阻電機減振方法。

背景技術：

無軸承開關磁阻電機突破了傳統電機采用機械軸承支撐轉子的框架，其利用電力電子和微機控制技術主動控制定子繞組的電流，從而改變施加于轉子上的電磁力，使電機同時具備驅動和自懸浮能力，無軸承開關磁阻電機除了保留開關磁阻電機的固有優勢外，同時解決了電機長時間運行帶來的磨損、潤滑等維護保養難題，使得開關磁阻電機的高速適用性更得以充分發揮，在航空、航天等領域具備應用前景。

無軸承開關磁阻電機雖為一種特殊的開關磁阻電機，但是無軸承開關磁阻電機仍然難以避免徑向電磁力帶來的定子振動問題，這個問題無軸承開關磁阻電機磁場特性復雜化，變得更加難以解決，為了解決這個問題，我們提出了一種無軸承的開關磁阻電機減振方法。

技術實現要素：

本發明的目的在于提供一種無軸承的開關磁阻電機減振方法，以解決上述背景技術中提出的問題。

為實現上述目的，本發明提供如下技術方案：一種無軸承的開關磁阻電機減振方法，所述無軸承的開關磁阻電機減振方法包括下述三個步驟：

第一步建立無軸承開關磁阻電機的相關參數的數學模型，本文以三相12/8極結構的無軸承開關磁阻電機為研究對象(下文中所述的電機均為三相12/8極結構的無軸承開關磁阻電機)；

第二步建立計算流程圖和系統控制框圖，使得整個電機減振步驟流程清晰明了；

第三步通過仿真和實驗來驗證本發明對電機的減振效果。

優選的，第一步建立無軸承開關磁阻電機的相關參數的數學模型具體為：

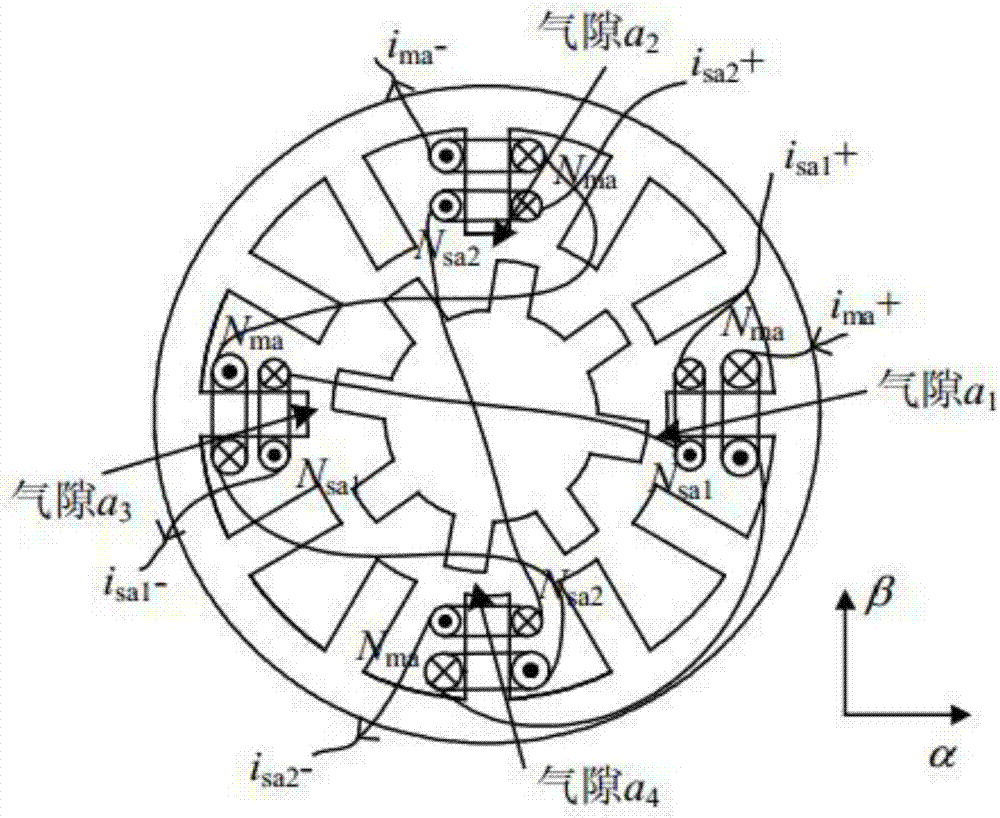
電機矩陣及懸浮力模型的建立，電機的轉子結構及a相繞組結構如圖1所示，當a相繞組通電時，產生的懸浮力和電子轉矩分別簡化表示為：

ta＝jt(θ)(2n²mi²ma+n²si²sa1+n²si²sa2)(2)

式中：fα、fβ為和方向瞬時懸浮力；ta為a相順時轉矩；nm、ns為任一個定子極的主繞組和懸浮繞組匝數；ima、isa1、isa2為a相繞組電流和α、β兩個方向的懸浮繞組電流；懸浮力系數kf(θ)和轉矩系數jt(θ)為電機結構參數和轉子位置角θ的函數；

定子極徑向力模型建立，應用麥克斯韋應力法原理，選擇圖2所示的積分路徑，定子極所受的徑向磁吸力表示為：

式中：h為轉子疊片長度；μ0為空氣磁導率；bm為定轉子極交疊部分氣隙(主氣隙)磁密；bf1和bf2均為邊緣氣隙磁密；bm、bf1和bf2都是θ的函數；

忽略磁飽和，由磁路法可得圖1中氣隙a1處的磁場主磁密bm(θ)和邊緣磁密bf1(θ)、bf2(θ)可以分別表示為：

bm(θ)＝μ0(nmima+nsisa1)/l0(4)

bf1(θ)≈bf2(θ)＝μ0(nmima+nsisa1)/(l0+πr|θ|/4)(5)

式中r為轉子極半徑。

聯立公式3和公式5，可得fsrα＝ksf(θ)(nmima+nsisal)²(6)

式中：fsr為氣隙a1處對應的a相定子極(a相α正方向所在位置的定子極)受到的瞬時徑向磁吸力，定子徑向磁吸力系數ksf(θ)為電機結構參數和轉子位置角θ的函數，可以表示為：

同理可得，氣隙a2處對應的a相定子極(a相β正方向所在位置的定子極)受到的瞬時徑向磁吸力fsrβ可以表示為：

fsrβ＝ksf(θ)(nmima+nsisa2)(7)

優選的，第二步建立計算流程圖和系統控制框圖具體為：本文為了減小定子振動，在保證電機轉子懸浮所需懸浮力一定的前提下，需要盡量減少定子極受到的徑向電磁力，以這一目標推導控制策略的約束條件，根據公式6和公式7，有如下不等式成立：

fsrα≥4ksf(θ)nmnsimaisa1(8)

fsrβ≥4ksf(θ)nmnsimaisa2(9)

當|fsrα|取最小值時，有：nmima＝nsisa1(10)

當|fsrβ|取最小值時，有：nmima＝nsisa2(11)

對于圖1所示電機，每相主繞組由4個定子極上的線圈串聯而成，而α和β方向所需的懸浮力不可能每時每刻都相同，所以式10和式11不可能同時成立，為了兼顧兩者，可對式10、11取平均值；

數學中取平均值的常用方法有算術平均值、均方根平均值和幾何平均值，對公式10和公式11分別取上述平均值，結果如圖3所示；

從圖3中的nmima取值的三種表達式可以看出，當α和β兩個方向所需的懸浮力相等或比較接近時，即有兩方向的懸浮繞組安匝數需求基本相等或接近，這時3種方法完全等效，所得的主繞組電流一致；在上述假定的特殊情況下isa1≈isa2，即公式10和公式11同時成立；實際上，大部分清涼下兩個方向所需的懸浮力是不相等的，因此比較3種方法的優劣主要是當兩個方向的懸浮力不相等時，對定子極徑向力的減小程度；

根據數學規律，有以下不等式成立：

取算術平均值的結果是，主繞組安匝數在兩個方向的懸浮繞組安匝數的中間，即和兩者差值的絕對值相等，這種方法在實際中遇到兩個方向懸浮力相差較大，即兩個方向的懸浮繞組安匝數相差較大時，會使得主繞組安匝數和兩個懸浮繞組安匝數的差值都比較大，因此兼顧兩個方向的結果是兩個方向都可能起不到較好的減小定子極磁吸力的作用；

均方根平均值和幾何平均值的結果是，主繞組安匝數在兩個方向的懸浮繞組安匝數之間，從公式12可以看出，前者結果更趨向于較大的一方，后者結果更趨向于較小的一方。在實際的控制過程中，由位移反饋經pid調節得到懸浮力，在所需懸浮力較小的一個方向上，此時該方向的徑向位移很小，計算出來的懸浮繞組電流也較小，因此即使不滿足公式10或公式11的關系，此時定子極受到的徑向力也較小，不會導致太大的定子振動，因此優先保證徑向力給定較大的一方；而且為了保證提供的懸浮力能使轉子穩定懸浮，而不致使懸浮繞組電流太大，同樣要求優先保證所需懸浮力較大的一個方向，因此選擇第二種取均方根平均值的方法，即公式13為約束條件，來確定電機的減振控制策略：

控制參數的計算：為了簡化控制，本文選擇每相導通15度的單相控制策略，得出公式13的約束條件后，減振控制策略確定參數就是由公式1、公式2和公式13計算確定主繞組、懸浮繞組電流及超前角；

將公式1和公式13代入公式2.可得順時轉矩的表達式：

對公式14所示的順時轉矩在一個周期內求平均，可得平均電磁轉矩：

tavg＝gtf(θm)f(15)

其中：

公式15中gtf(θm)是電機參數和超前角θm的函數，因此，在懸浮力和平均轉矩給定的情況下就可以由公式15計算出超前角θm，而要滿足每相導通15度的要求，θm不能大于7.5度，但是當電機給定的平均轉矩較大時有可能出現計算結果θm＞7.5度的情況，因此，下文分兩種情況進行討論：

1)0°≤m≤7.5°

此時，直接由公式13和公式16可得：

進一步，由公式1和公式16可得isa1和isa2；

2)θm＞7.5°

此時，令θm＝7.5°，但將超前角取最大值7.5°后，公式13不成立，因此必須重新設定約束條件，為了減小振動，此時將公式13表示的約束條件修改為的絕對值最小；

此時，平均轉矩的表達式可以表示為：

式中cm(θm)是電機參數和超前角θm的函數，由公式18可得：

進一步，由公式1和公式16可得到isa1和isa2；

綜上所示，可以確定電機控制參數的流程圖如圖4所示，圖5為振動控制策略框圖，光電傳感器檢測出轉子的位置信號，通過算計得到電機的實時轉速，其與給定轉速的差值經pi調節得到平均轉軍的給定值tavg，電渦流傳感器將兩個方向的徑向位移轉換為電信號，經pid調節得到懸浮力的給定值和然后，通過減振控制策略計算參數的方法解算出開通角θon、關斷角θoff，主繞組電流i及懸浮繞組電流和最后，通過兩套繞組的功率變換器實時跟蹤電流給定值，從而實現電機的穩定懸浮運行。

優選的，第三步通過仿真和實驗來驗證本發明對電機的減振效果具體為：根據上述控制算法，通過系統仿真來驗證其有效性，仿真采用的樣機參數如圖6所示；

考慮到電機的高速性能及徑向懸浮性能，本文樣機設計的額定轉矩為tn＝0.6n.m，仿真時，設定兩個方向的徑向懸浮力給定值分別為40n和30n，首先，在平均轉矩給定值為0.05n.m下進行仿真分析，通過系統仿真得到主繞組和懸浮繞組電流分布圖，然后通過有限元計算得到瞬時轉矩和懸浮力的分布圖，圖7、圖8分別為采用本文振動控制策略和采用傳統方波控制策略得到的轉子一個旋轉周期的仿真結果，從圖7可以看出，減振控制策略的主繞組電流不再為方波形式，而是通過控制算法實時計算得到，其可以為電機提供所需的轉矩和懸浮力，本文給出了a相對應4個方向處定子極所受的徑向力分布圖為例，包括兩個正方向的fsrα+、fsrβ+和兩個負方向的fsα-、fsrβ-，b、c兩相導通時相應定子極受到的徑向力分布圖和a相導通時類似，為了對比，將圖7和圖8中虛線圈部分表示的a相兩個正方向定子極徑向力放大，如圖9所示，從圖9可以看出，減振控制策略下a相兩個正方向位置的定子極徑向力fsrα+和fsrβ+在整個周期里都小于傳統控制策略，而且脈動較小，從圖7可以看出，減振控制策略下，fsα-、fsrβ-在整個周期內都接近于0，fsrd-的最大值只有約0.15n，fsrβ-的最大值只有約0.21n；從圖8可以看出，傳統控制策略下的fsrα-和fsrβ-除了一小段徑向力接近于0，整個周期里的大部分位置都明顯比減振控制策大，fsrα-的最大值為5.59n，fsrβ-的最大值為3.25n；可見，新的減振控制策略可以減小定子的電磁振動，保持徑向懸浮力給定值分別為40n和30n不變，加大平均轉矩給定值為0.5n.m進行仿真分析，圖10為分析得到的a相兩個正方向的定子極徑向力波形和瞬時轉矩波形，由于兩個負方向的定子極徑向力和輕載時一樣都非常小，不會激起定子振動，所以在此未給出，從圖9可以看出，轉矩的增大使得兩種控制策略的超前角都比輕載時增大，在定轉子極接近重合位置，即定子極徑向力較大的位置，包括換相關斷時，其徑向力均明顯小于傳統控制策略，有利于減小定子的電磁振動，而負載加大后，在定轉子極遠離對齊位置時，有一段角度位置處減振控制策略下定子極受到的徑向力較傳統控制策略時要大，但由于此時電機氣隙較大，徑向力本身較小，也不致激起較大的振動，反而正是由于這一段徑向力的增大而使得減振控制策略在整個周期的徑向力變化更為平緩，這也是有利于減振降噪的一個因素，因此加大負載同樣可以得到新的控制策略利于減小定子振動的結論。

與現有技術相比，本發明的有益效果是：本發明以主動控制無軸承開關磁阻電機的定子振動為目的，研究了一種無軸承的開關磁阻電機減振方法，通過理論分析、仿真和實驗相結合的方法對新型控制策略和傳統控制策略下無軸承的開關磁阻電機的定子振動進行了比較，驗證減振方法的可行性，減小無軸承開關磁阻電機的振動。

附圖說明

圖1為本專利中無軸承的開關磁阻電機結構示意圖；

圖2為本專利中定子極徑向計算積分路徑圖；

圖3為本專利中取平均值的方法示意圖；

圖4為本專利中電流和超前角計算流程圖；

圖5為本專利中振動控制策略框圖；

圖6為本專利中仿真用樣機參數示意圖；

圖7為本專利中減振控制策略一個周期的懸浮力、轉矩、定子極向及電流波形示意圖；

圖8為本專利中傳統控制策略一個周期的懸浮力、轉矩、定子極向及電流波形示意圖；

圖9為本專利中定子極徑向力波形示意圖；

圖10為本專利中定子極徑向力和順時轉矩波形示意圖。

具體實施方式

下面將結合具體實施例對本發明進行進一步描述，但本發明的保護范圍并不限于此。

一種無軸承的開關磁阻電機減振方法，所述無軸承的開關磁阻電機減振方法包括下述三個步驟：

第一步建立無軸承開關磁阻電機的相關參數的數學模型，本文以三相12/8極結構的無軸承開關磁阻電機為研究對象(下文中所述的電機均為三相12/8極結構的無軸承開關磁阻電機)；

第二步建立計算流程圖和系統控制框圖，使得整個電機減振步驟流程清晰明了；

第三步通過仿真和實驗來驗證本發明對電機的減振效果。

具體而言，第一步建立無軸承開關磁阻電機的相關參數的數學模型具體為：

電機矩陣及懸浮力模型的建立，電機的轉子結構及a相繞組結構如圖1所示，當a相繞組通電時，產生的懸浮力和電子轉矩分別簡化表示為：

ta＝jt(θ)(2n²mi²ma+n²si²sa1+n²si²sa2)(2)

式中：fα、fβ為和方向瞬時懸浮力；ta為a相順時轉矩；nm、ns為任一個定子極的主繞組和懸浮繞組匝數；ima、isa1、isa2為a相繞組電流和α、β兩個方向的懸浮繞組電流；懸浮力系數kf(θ)和轉矩系數jt(θ)為電機結構參數和轉子位置角θ的函數；

定子極徑向力模型建立，應用麥克斯韋應力法原理，選擇圖2所示的積分路徑，定子極所受的徑向磁吸力表示為：

式中：h為轉子疊片長度；μ0為空氣磁導率；bm為定轉子極交疊部分氣隙(主氣隙)磁密；bf1和bf2均為邊緣氣隙磁密；bm、bf1和bf2都是θ的函數；

忽略磁飽和，由磁路法可得圖1中氣隙a1處的磁場主磁密bm(θ)和邊緣磁密bf1(θ)、bf2(θ)可以分別表示為：

bm(θ)＝μ0(nmima+nsisa1)/l0(4)

bf1(θ)≈bf2(θ)＝μ0(nmima+nsisa1)/(l0+πr|θ|/4)(5)

式中r為轉子極半徑。

聯立公式3和公式5，可得fsrα＝ksf(θ)(nmima+nsisa1)²(6)

式中：fsr為氣隙a1處對應的a相定子極(a相α正方向所在位置的定子極)受到的瞬時徑向磁吸力，定子徑向磁吸力系數ksf(θ)為電機結構參數和轉子位置角θ的函數，可以表示為：

同理可得，氣隙a2處對應的a相定子極(a相β正方向所在位置的定子極)受到的瞬時徑向磁吸力fsrβ可以表示為：

fsrβ＝ksf(θ)(nmima+nsisa2)(7)

具體而言，第二步建立計算流程圖和系統控制框圖具體為：本文為了減小定子振動，在保證電機轉子懸浮所需懸浮力一定的前提下，需要盡量減少定子極受到的徑向電磁力，以這一目標推導控制策略的約束條件，根據公式6和公式7，有如下不等式成立：

fsrα≥4ksf(θ)nmnsimaisa1(8)

fsrβ≥4ksf(θ)nmnsimaisa2(9)

當|fsrα|取最小值時，有：nmima＝nsisa1(10)

當|fsrβ|取最小值時，有：nmima＝nsisa2(11)

對于圖1所示電機，每相主繞組由4個定子極上的線圈串聯而成，而α和β方向所需的懸浮力不可能每時每刻都相同，所以式10和式11不可能同時成立，為了兼顧兩者，可對式10、11取平均值；

數學中取平均值的常用方法有算術平均值、均方根平均值和幾何平均值，對公式10和公式11分別取上述平均值，結果如圖3所示；

從圖3中的nmima取值的三種表達式可以看出，當α和β兩個方向所需的懸浮力相等或比較接近時，即有兩方向的懸浮繞組安匝數需求基本相等或接近，這時3種方法完全等效，所得的主繞組電流一致；在上述假定的特殊情況下isa1≈isa2，即公式10和公式11同時成立；實際上，大部分清涼下兩個方向所需的懸浮力是不相等的，因此比較3種方法的優劣主要是當兩個方向的懸浮力不相等時，對定子極徑向力的減小程度；

根據數學規律，有以下不等式成立：

取算術平均值的結果是，主繞組安匝數在兩個方向的懸浮繞組安匝數的中間，即和兩者差值的絕對值相等，這種方法在實際中遇到兩個方向懸浮力相差較大，即兩個方向的懸浮繞組安匝數相差較大時，會使得主繞組安匝數和兩個懸浮繞組安匝數的差值都比較大，因此兼顧兩個方向的結果是兩個方向都可能起不到較好的減小定子極磁吸力的作用；

均方根平均值和幾何平均值的結果是，主繞組安匝數在兩個方向的懸浮繞組安匝數之間，從公式12可以看出，前者結果更趨向于較大的一方，后者結果更趨向于較小的一方。在實際的控制過程中，由位移反饋經pid調節得到懸浮力，在所需懸浮力較小的一個方向上，此時該方向的徑向位移很小，計算出來的懸浮繞組電流也較小，因此即使不滿足公式10或公式11的關系，此時定子極受到的徑向力也較小，不會導致太大的定子振動，因此優先保證徑向力給定較大的一方；而且為了保證提供的懸浮力能使轉子穩定懸浮，而不致使懸浮繞組電流太大，同樣要求優先保證所需懸浮力較大的一個方向，因此選擇第二種取均方根平均值的方法，即公式13為約束條件，來確定電機的減振控制策略：

控制參數的計算：為了簡化控制，本文選擇每相導通15度的單相控制策略，得出公式13的約束條件后，減振控制策略確定參數就是由公式1、公式2和公式13計算確定主繞組、懸浮繞組電流及超前角；

將公式1和公式13代入公式2.可得順時轉矩的表達式：

對公式14所示的順時轉矩在一個周期內求平均，可得平均電磁轉矩：

tavg＝gtf(θm)f(15)

其中：

公式15中gtf(θm)是電機參數和超前角θm的函數，因此，在懸浮力和平均轉矩給定的情況下就可以由公式15計算出超前角θm，而要滿足每相導通15度的要求，θm不能大于7.5度，但是當電機給定的平均轉矩較大時有可能出現計算結果θm＞7.5度的情況，因此，下文分兩種情況進行討論：

1)0°≤m≤7.5°

此時，直接由公式13和公式16可得：

進一步，由公式1和公式16可得isa1和isa2；

2)θm＞7.5°

此時，令θm＝7.5°，但將超前角取最大值7.5°后，公式13不成立，因此必須重新設定約束條件，為了減小振動，此時將公式13表示的約束條件修改為的絕對值最小；

此時，平均轉矩的表達式可以表示為：

式中cm(θm)是電機參數和超前角θm的函數，由公式18可得：

進一步，由公式1和公式16可得到isa1和isa2；

綜上所示，可以確定電機控制參數的流程圖如圖4所示，圖5為振動控制策略框圖，光電傳感器檢測出轉子的位置信號，通過算計得到電機的實時轉速，其與給定轉速的差值經pi調節得到平均轉軍的給定值tavg，電渦流傳感器將兩個方向的徑向位移轉換為電信號，經pid調節得到懸浮力的給定值和然后，通過減振控制策略計算參數的方法解算出開通角θon、關斷角θoff，主繞組電流i及懸浮繞組電流和最后，通過兩套繞組的功率變換器實時跟蹤電流給定值，從而實現電機的穩定懸浮運行。

具體而言，第三步通過仿真和實驗來驗證本發明對電機的減振效果具體為：根據上述控制算法，通過系統仿真來驗證其有效性，仿真采用的樣機參數如圖6所示；

考慮到bsrm的高速性能及徑向懸浮性能，本文樣機設計的額定轉矩為tn＝0.6n.m，仿真時，設定兩個方向的徑向懸浮力給定值分別為40n和30n，首先，在平均轉矩給定值為0.05n.m下進行仿真分析，通過系統仿真得到主繞組和懸浮繞組電流分布圖，然后通過有限元計算得到瞬時轉矩和懸浮力的分布圖，圖7、圖8分別為采用本文振動控制策略和采用傳統方波控制策略得到的轉子一個旋轉周期的仿真結果，從圖7可以看出，減振控制策略的主繞組電流不再為方波形式，而是通過控制算法實時計算得到，其可以為電機提供所需的轉矩和懸浮力，本文給出了a相對應4個方向處定子極所受的徑向力分布圖為例，包括兩個正方向的fsrα+、fsrβ+和兩個負方向的fsα-、fsrβ-，b、c兩相導通時相應定子極受到的徑向力分布圖和a相導通時類似，為了對比，將圖7和圖8中虛線圈部分表示的a相兩個正方向定子極徑向力放大，如圖9所示，從圖9可以看出，減振控制策略下a相兩個正方向位置的定子極徑向力fsrα+和fsrβ+在整個周期里都小于傳統控制策略，而且脈動較小，從圖7可以看出，減振控制策略下，fsα-、fsrβ-在整個周期內都接近于0，fsrα-的最大值只有約0.15n，fsrβ-的最大值只有約0.21n；從圖8可以看出，傳統控制策略下的fsrα-和fsrβ-除了一小段徑向力接近于0，整個周期里的大部分位置都明顯比減振控制策略大，fsrα-的最大值為5.59n，fsrβ-的最大值為3.25n；可見，新的減振控制策略可以減小定子的電磁振動，保持徑向懸浮力給定值分別為40n和30n不變，加大平均轉矩給定值為0.5n.m進行仿真分析，圖9為分析得到的a相兩個正方向的定子極徑向力波形和瞬時轉矩波形，由于兩個負方向的定子極徑向力和輕載時一樣都非常小，不會激起定子振動，所以在此未給出，從圖9可以看出，轉矩的增大使得兩種控制策略的超前角都比輕載時增大，在定轉子極接近重合位置，即定子極徑向力較大的位置，包括換相關斷時，其徑向力均明顯小于傳統控制策略，有利于減小定子的電磁振動，而負載加大后，在定轉子極遠離對齊位置時，有一段角度位置處減振控制策略下定子極受到的徑向力較傳統控制策略時要大，但由于此時電機氣隙較大，徑向力本身較小，也不致激起較大的振動，反而正是由于這一段徑向力的增大而使得減振控制策略在整個周期的徑向力變化更為平緩，這也是有利于減振降噪的一個因素，因此加大負載同樣可以得到新的控制策略利于減小定子振動的結論。

工作原理：首先建立無軸承開關磁阻電機的相關參數的數學模型，然后以減少無軸承開關磁阻電機定子振動為目標設計解決方案，建立方案的計算流程圖和系統控制框圖，最后通過仿真和實驗來驗證本發明應用方案對無軸承開關磁阻電機的減振效果，對比傳統控制策略下無軸承的開關磁阻電機的定子振動，驗證本方案實施的減振方法的可行性，有效的減小了無軸承開關磁阻電機的振動。

以上所述，僅為本發明較佳的具體實施方式，但本發明的保護范圍并不局限于此，任何熟悉本技術領域的技術人員在本發明揭露的技術范圍內，根據本發明的技術方案及其發明構思加以等同替換或改變，都應涵蓋在本發明的保護范圍之內。