本發明涉及載臂無人機路徑規劃，具體涉及一種基于微分平坦的載臂移動平臺的路徑規劃方法及系統。

背景技術：

1、微分平坦是控制系統的特殊性質，是非線性控制系統中“能控性”的一種體現。具有微分平坦性質的系統的輸入可以通過已知的、所需的輸出信號精確地計算得出。這在無人機類機器人的運動規劃中是很好的性質，因為對于具有微分平坦性質的系統，可以避免在其復雜的動力學模型上進行控制器設計，而是通過規劃出光滑的運動路徑，通過運動路徑直接解算出輸入控制量。

2、informedrrt*(informed?rapidly-exploring?random?tree?star)算法是一種路徑規劃算法，旨在提高路徑優化的效率。它是對rrt算法的改進，通過限制采樣范圍來加速找到最優路徑的過程。在找到一條初始路徑后，informed?rrt會將采樣范圍限制在一個橢圓區域內，這個橢圓的焦點是起點和終點，長軸是當前路徑的長度，短軸是起點和終點之間的直線距離。橢圓采樣的目的是減少無效的采樣點，從而更快地找到更優的路徑。隨著找到更短的路徑，橢圓的長軸會逐漸縮短，進一步集中采樣點。informedrrt繼承了rrt的漸進最優性，即隨著時間的推移和采樣點的增加，找到的路徑會逐漸接近最優。informed?rrt通過集中采樣在潛在的最優路徑區域內，大大提高了路徑優化的效率，減少了計算時間。這使得informedrrt特別適用于高維空間中的路徑規劃問題，如機器人導航、自動駕駛和無人機路徑規劃等。

3、閉式求解的minimum?snap算法是一種用于生成平滑軌跡的優化技術，特別適用于無人機和機器人等需要高精度運動控制的系統。該算法旨在通過多項式擬合生成一條滿足動力學約束的軌跡，并在位置、速度、加速度等方面具有高階連續性。通過這種閉式求解的minimum?snap算法，可以生成一條平滑且滿足動力學約束的軌跡，廣泛應用于無人機、機器人等領域。具體應用中，minimum?snap算法不僅能夠生成平滑的軌跡，還能確保軌跡在動力學上的可行性，從而提高系統的穩定性和控制精度。

4、但是，現有的載臂無人機運動規劃方法中模型解耦合困難，傳統解耦后的規劃算法需要并行運算，導致機載計算平臺計算壓力過大進而使得載臂無人機響應性能下降。

技術實現思路

1、鑒于以上問題，本發明提出一種基于微分平坦的載臂移動平臺的路徑規劃方法及系統。

2、根據本發明的一方面，提出一種基于微分平坦的載臂移動平臺的路徑規劃方法，該方法包括：

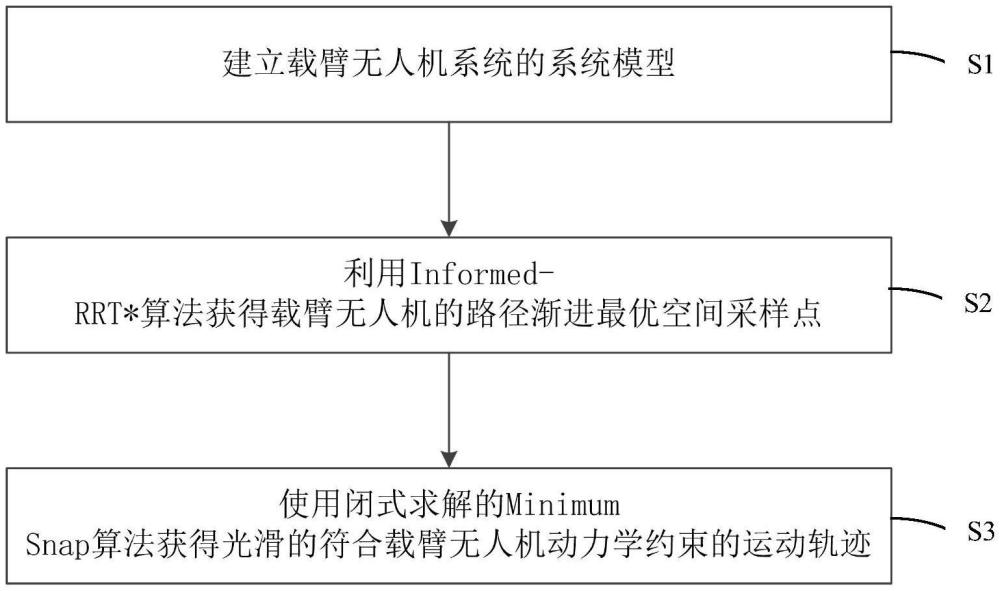
3、建立載臂無人機系統的系統模型；

4、利用informed-rrt*算法獲得載臂無人機的路徑漸進最優空間采樣點；

5、使用閉式求解的minimum?snap算法獲得光滑的符合載臂無人機動力學約束的運動軌跡。

6、進一步地，所述載臂無人機系統的系統模型建立如下：

7、

8、式中，為系統的狀態變量，p,l分別為系統的廣義動量和角動量；φ,θ,ψ分別為滾轉角，俯仰角和偏航角；η為由機械臂關節角組成的向量；表示系統的控制輸入，表示機械臂各個關節力矩，t表示多旋翼無人機產生的推力，τφ,τθ,τψ分別表示滾轉、俯仰、偏航扭矩；f(q)表示漂移向量函數；表示驅動矩陣函數。

9、進一步地，所述載臂無人機系統具有微分平坦性質，所述微分平坦性質具體為：除在奇點以及t＝0外，向量是載臂無人機系統的平坦輸出，其中表示由地面坐標系到基底坐標系的旋轉矩陣。

10、進一步地，所述利用informed-rrt*算法獲得載臂無人機的路徑漸進最優空間采樣點包括：

11、初始化定義起始點、目標點、步長、最大迭代次數、一棵空搜索樹，并將起始點作為樹的根節點；計算起始點和目標點之間的直線距離cmin，初始化一個以起始點和終點為焦點的橢圓形搜索空間，橢圓的長軸為直線距離cmin；

12、在每一次迭代中，按照下述步驟順序執行：

13、采樣：在橢圓形搜索空間內隨機采樣一個點xrand；

14、尋找最近點：在搜索樹中找到距離xrand最近的節點xnear；

15、連接：從節點xnear向節點xrand方向延伸步長，得到新節點xnew；檢查節點xnear和新節點xnew之間的路徑是否與障礙物碰撞，若無碰撞，則將新節點xnew添加到搜索樹中，并設置節點xnear為新節點xnew的父節點；

16、重連：以新節點xnew為中心，在一定范圍內搜索樹中的節點；對于搜索到的每個節點x′near，計算從起始點x0到節點xnew再到新節點x′near的路徑代價c(x0,xnew)+c(xnew,x′near)；如果新的路徑代價小于節點x′near原來的路徑代價c(x0,x′near)，則更新節點x′near的父節點為新節點xnew，并更新搜索樹t的連接關系；其中c(a,b)為代價函數，定義為a,b兩點間的歐氏距離；

17、檢查目標：如果新節點xnew與目標點之間的距離小于設定的閾值，則算法結束，返回找到的路徑；

18、直到達到最大迭代次數或找到一條可行路徑則迭代終止。

19、進一步地，所述使用閉式求解的minimum?snap算法獲得光滑的符合載臂無人機動力學約束的運動軌跡包括：

20、將informed-rrt*算法獲得的多個采樣點輸入閉式求解的minimum?snap算法，確定軌跡的階數，選擇五次多項式，并根據時間分配構建約束矩陣，將每段軌跡的起點和終點的位置信息、速度信息和加速度信息轉化為矩陣形式；構造映射矩陣，將連續性約束轉化為矩陣形式；構造置換矩陣，將已知的約束條件和未知的自由變量分開；通過矩陣運算求解每段軌跡的多項式系數，生成最終的軌跡。

21、進一步地，所述使用閉式求解的minimum?snap算法獲得光滑的符合載臂無人機動力學約束的運動軌跡的具體過程包括：

22、最終生成的一條經過已知采樣點且滿足約束的分段多項式軌跡的軌跡方程寫為：

23、

24、其中，pj,i,j＝1,…,m,i＝1,…,n為多項式系數，t表示當前時刻，每段軌跡f1、f2、…、fm都是多項式軌跡，t0,…,tm均為已知的到達對應采樣點的時刻，m為采樣點個數；n表示多項式軌跡的次數；

25、在每個分段軌跡起始點和終點滿足以下微分約束：

26、ampm＝dm

27、其中，am為約束矩陣，dm為具體約束的值；pm表示第m段軌跡的多項式系數；

28、在每個采樣點的前后兩段多項式軌跡滿足以下連續性、光滑性約束：

29、

30、代價函數為：

31、

32、其中：

33、

34、則帶約束的qp問題為：

35、

36、分離約束中的自由變量df和確定變量dp，將以上帶約束的qp問題轉化為如下無約束的qp問題：

37、

38、其中，c定義來源于r＝ca-tqa-1ct；

39、對j關于dp求導取得的極值點即為全局最優點將代回c,a即獲得最終的全局最優的各個多項式系數：將p代回多項式軌跡方程即獲得滿足約束的光滑軌跡。

40、根據本發明的另一方面，提出一種基于微分平坦的載臂移動平臺的路徑規劃系統，該系統包括：

41、模型建立模塊，其配置成建立載臂無人機系統的系統模型；

42、最優采樣點計算模塊，其配置成利用informed-rrt*算法獲得載臂無人機的路徑漸進最優空間采樣點；

43、軌跡生成模塊，其配置成使用閉式求解的minimum?snap算法獲得光滑的符合載臂無人機動力學約束的運動軌跡。

44、進一步地，所述模型建立模塊中載臂無人機系統的系統模型建立如下：

45、

46、式中，為系統的狀態變量，p,l分別為系統的廣義動量和角動量；φ,θ,ψ分別為滾轉角，俯仰角和偏航角；η為由機械臂關節角組成的向量；表示系統的控制輸入，表示機械臂各個關節力矩，t表示多旋翼無人機產生的推力，τφ,τθ,τψ分別表示滾轉、俯仰、偏航扭矩；f(q)表示漂移向量函數；表示驅動矩陣函數；

47、所述載臂無人機系統具有微分平坦性質，所述微分平坦性質具體為：除在奇點以及t＝0外，向量是載臂無人機系統的平坦輸出，其中表示由地面坐標系到基底坐標系的旋轉矩陣。

48、進一步地，所述最優采樣點計算模塊中所述利用informed-rrt*算法獲得載臂無人機的路徑漸進最優空間采樣點包括：

49、初始化定義起始點、目標點、步長、最大迭代次數、一棵空搜索樹，并將起始點作為樹的根節點；計算起始點和目標點之間的直線距離cmin，初始化一個以起始點和終點為焦點的橢圓形搜索空間，橢圓的長軸為直線距離cmin；

50、在每一次迭代中，按照下述步驟順序執行：

51、采樣：在橢圓形搜索空間內隨機采樣一個點xrand；

52、尋找最近點：在搜索樹中找到距離xrand最近的節點xnear；

53、連接：從節點xnear向節點xrand方向延伸步長，得到新節點xnew；檢查節點xnear和新節點xnew之間的路徑是否與障礙物碰撞，若無碰撞，則將新節點xnew添加到搜索樹中，并設置節點xnear為新節點xnew的父節點；

54、重連：以新節點xnew為中心，在一定范圍內搜索樹中的節點；對于搜索到的每個節點x′near，計算從起始點x0到節點xnew再到新節點x′near的路徑代價c(x0,xnew)+c(xnew,x′near)；如果新的路徑代價小于節點x′near原來的路徑代價c(x0,x′near)，則更新節點x′near的父節點為新節點xnew，并更新搜索樹t的連接關系；其中c(a,b)為代價函數，定義為a,b兩點間的歐氏距離；

55、檢查目標：如果新節點xnew與目標點之間的距離小于設定的閾值，則算法結束，返回找到的路徑；

56、直到達到最大迭代次數或找到一條可行路徑則迭代終止。

57、進一步地，所述軌跡生成模塊中所述使用閉式求解的minimum?snap算法獲得光滑的符合載臂無人機動力學約束的運動軌跡包括：

58、將informed-rrt*算法獲得的多個采樣點輸入閉式求解的minimum?snap算法，確定軌跡的階數，選擇五次多項式，并根據時間分配構建約束矩陣，將每段軌跡的起點和終點的位置信息、速度信息和加速度信息轉化為矩陣形式；構造映射矩陣，將連續性約束轉化為矩陣形式；構造置換矩陣，將已知的約束條件和未知的自由變量分開；通過矩陣運算求解每段軌跡的多項式系數，生成最終的軌跡；具體過程包括：

59、最終生成的一條經過已知采樣點且滿足約束的分段多項式軌跡的軌跡方程寫為：

60、

61、其中，pj,i,j＝1,…,m,i＝1,…,n為多項式系數，t表示當前時刻，每段軌跡f1、f2、…、fm都是多項式軌跡，t0,…,tm均為已知的到達對應采樣點的時刻，m為采樣點個數；n表示多項式軌跡的次數；

62、在每個分段軌跡起始點和終點滿足以下微分約束：

63、ampm＝dm

64、其中，am為約束矩陣，dm為具體約束的值；pm表示第m段軌跡的多項式系數；

65、在每個采樣點的前后兩段多項式軌跡滿足以下連續性、光滑性約束：

66、

67、代價函數為：

68、

69、其中：

70、

71、

72、則帶約束的qp問題為：

73、

74、分離約束中的自由變量df和確定變量dp，將以上帶約束的qp問題轉化為如下無約束的qp問題：

75、

76、其中，c定義來源于r＝ca-tqa-1ct；

77、對j關于dp求導取得的極值點即為全局最優點將代回c,a即獲得最終的全局最優的各個多項式系數：將p代回多項式軌跡方程即獲得滿足約束的光滑軌跡。

78、本發明的有益技術效果是：

79、針對載臂無人機運動規劃算法中模型解耦合困難，傳統解耦后的規劃算法需要并行運算，提高機載計算平臺計算壓力使得載臂無人機響應性能下降的問題，本發明提出了一種基于載臂無人機微分平坦性質的、使用informed-rrt*算法獲得采樣點、使用閉式求解的minimum?snap算法獲得光滑的、可執行的軌跡的載臂無人機運動規劃方法。具體來說，本發明的有益效果為：

80、1)證明了載臂無人機系統的微分平坦特性，避免了對其運動學模型的解耦，使得在載臂無人機平臺上的運動規劃、控制、決策等課題可以更簡單、精確地求解，提升了載臂無人機平臺的易用性。

81、2)在高維空間中使用informed-rtt*算法對載臂無人機的基底無人機和機載機械臂進行一體化規劃，作為整體進行規劃優化，保證整體能量消耗最低，避免了多目標優化時會出現的無法同時全局最優情況，提高了總能量緊張的載臂無人機系統的能量利用效率。

82、3)使用閉式求解的minimum?snap算法進行光滑軌跡生成，提高了數值穩定性，避免在接近奇異點時出現無法求解的情況。