本發明涉及一種三穩態壓電懸臂梁結構俘能器的隨機控制方法，尤其涉及一種基于阻抗匹配與功率最大化原理針對隨機環境下三穩態俘能器的電路控制方法，屬于俘能器領域。

背景技術：

1、振動作為自然界中一種普遍存在的現象，鑒于其廣泛分布及蘊含的高能量密度特性，近幾十年來，關于如何將振動能量轉換并加以收集利用的研究逐漸興起。壓電振動俘能器可以采集環境中的機械能。懸臂梁結構因為其結構簡單穩定性高等優點，常被作為俘能器的機械結構。通過懸臂梁上壓電片的正壓電效應實現機械能到電能的轉換。振動能量采集在文獻中得到了廣泛的研究，結合彈簧-質量-阻尼系統的基本配置，共振時裝置的振動幅值可以明顯大于基座運動的振動幅值。早期的俘能器設計主要聚焦于窄帶頻率的線性能量轉換，然而激勵頻率偏離共振的任何偏差都可能導致發電的急劇減少，裝置的最佳性能被限制在基頻附近非常窄的帶寬內。在面臨寬頻譜振動能量源時，其效用顯著受限。為了克服傳統線性配置的這一問題，研究人員通過人為引入非線性恢復力來拓寬能量采集頻帶，提出了一系列非線性能量采集器的創新設計，涵蓋單穩態、雙穩態乃至三穩態的非線性振子結構。相較于線性采集器，非線性設計展現出三大顯著優勢：一是顯著拓寬了頻率響應范圍，使采集器能更有效地捕獲更廣泛頻率的振動能量；二是通過增強響應振幅，進一步提升了能量轉換效率；三是系統性地提高了輸出功率，為實際應用提供了更強的能源供給。

2、除了俘能器結構，能量管理電路也是影響俘能器輸出的重要因素。基于壓電式懸臂梁結構的俘能器輸出的能量具有不連續性和隨機性，如何讓電源管理電路跟隨能量采集器的工作模式實現最大功率傳輸是電源管理電路設計的關鍵問題之一。壓電能量采集系統電路主要由兩部分組成交流-直流和直流-交流部分，其中交流-直流部分有整流電路和接口電路。而dc-dc部分主要由開關變換器構成。研究人員ottman?g.k.等人最早提出了一種實現最佳功率傳輸的標準能量存儲電路，之后被稱為標準能量采集電路，但是該電路少阻抗匹配導致能量轉換效率較低。研究人員分別提出了同步電荷提取接口電路電路、并聯同步電感開關接口電路和串聯同步電感開關接口電路來提高機械能到電能轉換的效率，用來降低壓電能量采集器的功率損耗。為了實現最大能量傳輸，電源管理電路的設計必須與能量采集器的輸出特性和機電等效模型相契合。由于自然環境中振動的隨機性與俘能器的非線性，導致其能量采集器內部阻抗時刻變化，因此固定的阻抗匹配技術難以實現最大功率傳輸。研究人員kong?na等人使用微控制器單元執行了最大功率點跟蹤算法，通過動態電阻匹配實現，俘能器在47hz諧振頻率附近可獲得72％的功率效率。但是該算法是針對線性俘能器動態阻抗匹配設計，對于三穩態非線性俘能器同樣需要一種動態的功率最大化控制電路，以實現采集性能的提升。目前尚無針對隨機激勵下三穩態俘能器的功率最大化控制方法。

技術實現思路

1、本發明的目的是為了提高隨機激勵下三穩態俘能器的采集功率，提供了一種三穩態壓電懸臂梁結構俘能器的隨機控制方法；該方法利用數據驅動對三穩態非線性壓電懸臂梁式俘能器進行動力學建模，根據模型可以計算得到系統響應計算預測功率。基于預測功率和參考功率，使用模型預測控制方法對電路阻尼進行動態調整，得到最優匹配電阻值，進一步提高俘能器從隨機振源中俘獲電能的功率。

2、本發明的目的是通過以下技術方案實現的：

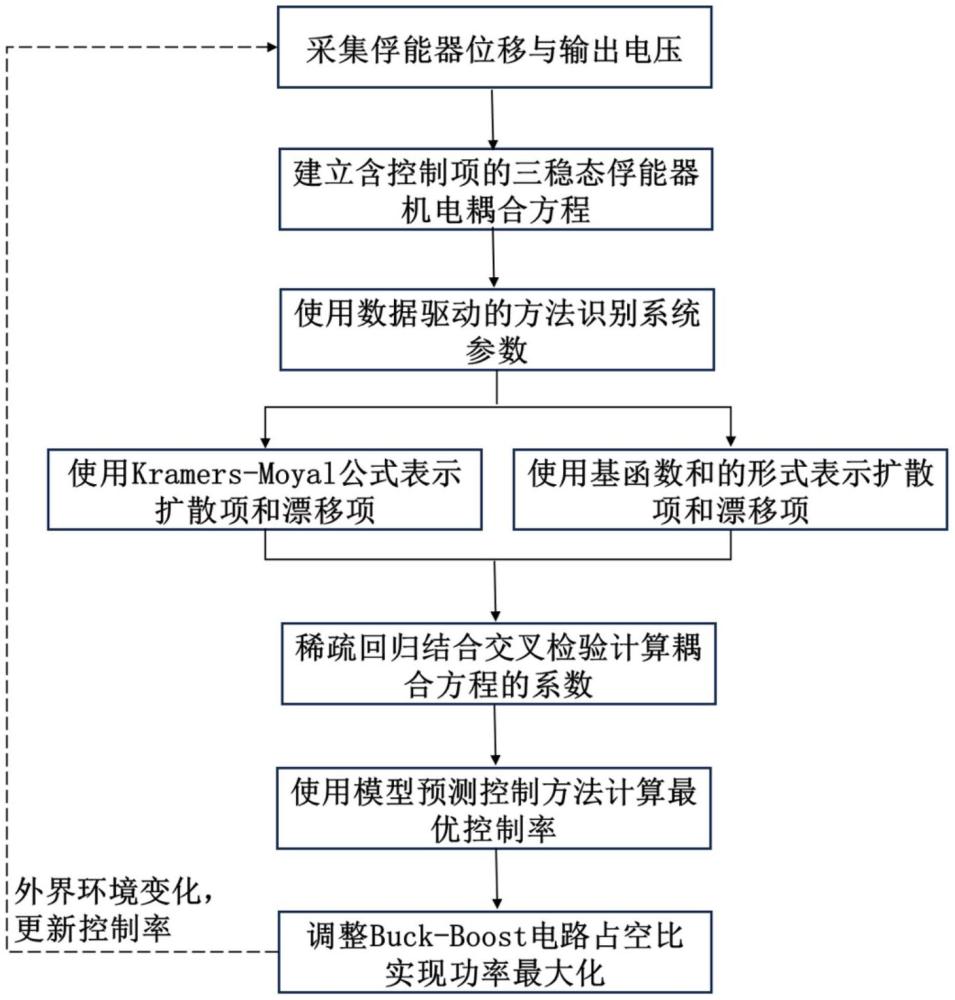
3、本發明公開三穩態壓電懸臂梁結構俘能器的隨機控制方法，考慮環境中的隨機激勵引入白噪聲激勵，通過俘能器的位移數據，利用數據驅動的非線性動力系統的稀疏辨識方法建立機電耦合三穩態俘能器的隨機系統模型。根據隨機系統的預測響應，使用模型預測控制方法設置合理的損失函數，能夠得任意強度噪聲激勵下三穩態俘能器的最優控制率，根據最優控制律α通過buck-boost電路施加控制信號，實現三穩態壓電懸臂梁結構俘能器的隨機控制，增大俘能器輸出功率。

4、本發明公開的三穩態壓電懸臂梁結構俘能器的隨機控制方法，包括如下步驟：

5、步驟一、考慮環境中的隨機激勵引入白噪聲，建立機電耦合的強非線性三穩態俘能器模型，并對所述俘能器模型進行無量綱化處理，得到機電耦合的強非線性三穩態俘能器無量綱化模型；

6、強非線性三穩態俘能器模型如式(1)所示：

7、

8、式中，表示尖端磁鐵的位移，表示壓電電壓，m表示尖端磁鐵的質量，表示時間，c表示阻尼系數，θ表示機電耦合系數，表示外界的隨機激勵，cp表示有效電容，表示電路的電阻；表示系統的勢能函數用多項式表示為：

9、

10、式中的為剛度系數；

11、引入下面的變換對系統方程式(1)進行無量綱化：

12、

13、其中為懸臂梁的固有頻率，為懸臂梁的長度尺度。t、x、v分別表示無量綱化的時間、位移和電壓；ζ、θ、α分別表示無量綱化的阻尼系數、機電耦合系數和機電時間常數比；km(m＝1,2,3)表示無量綱化后的剛度系數。

14、得到無量綱化后的強非線性三穩態俘能器機電耦合方程：

15、

16、式中，表示無量綱化的勢能函數，使用高斯白噪聲ξ(t)描述無量綱的外激勵，其統計特性中的均值和相關函數為：

17、e[ξ(t)]＝0，e[ξ(t)ξ(t+τ)]＝dδ(τ)；

18、e[·]表示對括號內的函數求均值，δ(τ)表示狄拉克函數，τ表示相關時間間隔，d為無量綱后的白噪聲的噪聲強度；

19、步驟二、基于采集到的三穩態俘能器的位移數據和電壓，使用非線性動力系統的稀疏辨識方法強非線性三穩態俘能器機電耦合方程中的無量綱系數ζ、θ、km(m＝1,2,3)、d，建立三穩態俘能器的模型方程。

20、強非線性三穩態俘能器機電耦合方程(3)改寫為隨機微分方程sdes：

21、

22、其中，y(t)為無量綱速度；b(t)是標準布朗運動；

23、采集時間[t1,t2,...,tn+1]對應的電壓[v1,v2,...,vn+1]和懸臂梁尖端位移[x1,x2,...,xn+1]，速度[y1,y2,...,yn]通過(xi+1-xi)/(ti+1-ti)(i＝1,2,...,n)計算得到，xi、yi和vi表示ti時刻對應的位移、速度和電壓，時間間隔為δt，n為采樣點個數。

24、式(4)中非零擴散項和漂移項表示為：

25、

26、漂移項a1中只包含速度yi且系數為1，不用對其系數進行辨識。對于漂移項a2，使用基函數φk和系數ck的乘積進行近似

27、

28、a2(xi,yi,vi)表示ti時刻對應的擴散漂移項，系數ck為基函數φk對應的系數。對于使用14個基函數，k＝1,...,14。

29、對于a3，使用基函數mj和系數pj的乘積進行近似

30、

31、a3(xi,yi,vi)表示ti時刻對應的擴散漂移項，系數pj為基函數mj對應的系數。對于使用15個基函數，j＝1,...,15。

32、對于b22，使用基函數ψr和系數qr的乘積進行近似

33、

34、b22(xi,yi)表示ti時刻對應的擴散漂移項，系數qr為基函數ψr對應的系數。對于使用6個基函數，r＝1,...,6。

35、根據kramers–moyal公式，漂移項a2、a3和非零擴散項b22表示為

36、

37、根據公式(7)和公式(12)的關系，得以下漂移項a2的系數求解的迭代方程：

38、ac＝b?(15)

39、其中

40、

41、c＝[c1,...,c14],

42、b＝[y2-y1,...,yn-yn-1]/δt.

43、a為由基函數φk(xi,yi,vi)組成的(n-1)×14維矩陣，c為由系數ck組成的向量，b為根據公式(12)計算的漂移項a2。

44、同理得漂移項a3的迭代方程為：

45、

46、其中

47、

48、p＝[p1,...,p15],

49、

50、為由基函數mj(xi,yi,vi)組成的(n-1)×15維矩陣，p為由系數pj組成的向量，為根據公式(13)計算的漂移項a3。

51、擴散項b22的迭代方程；

52、

53、其中

54、

55、q＝[q1,...,q6],

56、

57、為由基函數ψr(xi,yi,vi)組成的(n-1)×6維矩陣，q為由系數qr組成的向量，為根據公式(14)計算的漂移項b22。

58、使用sindy算法對系統參數進行求解；公式(15)用最小二乘方法進行化簡得因此公式(15)的解為

59、c＝(ata)-1(atb)?(18)

60、通過逐步稀疏回歸ssr算法從c中選擇具有最優稀疏度的解

61、公式(16)用最小二乘方法進行化簡得因此公式(16)的解為

62、

63、通過逐步稀疏回歸ssr算法從p中選擇具有最優稀疏度的解

64、公式(17)用最小二乘方法進行化簡得因此公式(17)的解為

65、

66、通過逐步稀疏回歸ssr算法從q中選擇具有最優稀疏度的解

67、具有最優稀疏度的解中包含無量綱系數ζ、θ、km(m＝1,2,3)，中包含無量綱系數α，中包含無量綱系數d；通過這一方法識別出具體的系統參數后，帶入方程(3)即可得到三穩態俘能器的模型方程。

68、步驟三、基于步驟二建立的三穩態俘能器的模型方程，求解系統響應，使用模型預測控制方法計算最優控制律α，根據最優控制律α通過buck-boost電路施加控制信號，實現三穩態壓電懸臂梁結構俘能器的隨機控制，增大俘能器輸出功率。

69、使用蒙特卡洛方法模擬俘能器系統輸出。使用四階龍格庫塔方法數值求解方程(3)，多次計算系統輸出求平均值得到均方電壓e[v2]；根據俘能器系統特性，無量綱化的系統輸出均方功率使用均方電壓表示為：

70、e[p]＝θαe[v2]?(21)

71、存在最優時間常數比α使系統輸出功率最大；然而對于受隨機激勵三穩態俘能器，最優α值不是固定值，使用控制方法獲得時變的控制率實現功率最大的效果；

72、式(21)即為系統響應公式。

73、計算0～tc時間內的最優控制律mc為控制時間步的個數，tc為控制時長，αl(l＝1,...,mc)為第l個時間步對應的控制參數，α為0～tc時間內控制參數的集合。

74、最優控制律通過計算時間內的最小損失函數獲得：

75、

76、其中mp為預測時間步的個數；為第k個預測步的預測功率，prefk為第k個預測步的參考功率，系數q為兩者差值的權重系數；αl為第l個控制步的控制信號，δαl為第l個控制步的控制信號變化率，rα為控制信號的權重，rδα為控制信號變化率的權重。

77、將功率作為預測響應，通過設定參考功率prefk得到令損失函數最小的最優控制率。通過buck-boost電路施加控制信號，實現三穩態壓電懸臂梁結構俘能器的隨機控制，使其輸出功率增大。

78、有益效果：

79、1、本發明公開的三穩態壓電懸臂梁結構俘能器的隨機控制方法，使用數據驅動的方法能夠智能識別系統參數完成機電耦合方程的建模，在具有控制項的情形下依然能夠完成系統的數字化建模，相較于現有的建模方法可以隨系統狀態改變進行對應的模型調整，能夠更加便利準確的實現控制。

80、2、本發明公開的三穩態壓電懸臂梁結構俘能器的隨機控制方法，基于阻抗匹配和功率最大化原理，通過調節電路的最優占空比達到阻抗匹配，實現功率最大化。本發明通過模型預測控制實現的，不但適應多種隨機環境，還克服非線性系統內阻難以匹配的問題。因此，相較于已有的阻抗匹配能量電路適應性更強。

81、3、本發明公開的三穩態壓電懸臂梁結構俘能器的隨機控制方法，除具有所述實現動態調整電路使輸出功率最大的有益效果外，實現三穩態俘能器的性能優化，控制信號收斂并對俘能器的優化設計提供重要參考。

82、4、本發明公開的三穩態壓電懸臂梁結構俘能器的隨機控制方法，考慮外界環境激勵為隨機激勵，更加真實模擬實際隨機環境，使本發明在實際應用中提升輸出功率的效果更加準確、真實。