本發明屬于仿生機器人技術領域，更具體地，涉及一種氣動肌肉的自適應控制方法和系統。

背景技術：

隨著氣動技術的發展，新型氣動元件及應用不斷涌現，氣動肌肉(pneumaticmuscle，pm)就是其中的典型代表。氣動肌肉與生物肌肉具有類似的力學特性，并且以其低成本、高功率/質量比、安裝簡便等方面的優勢而在醫療康復、遠程控制、智能機器人、工業自動化等領域得以廣泛應用。但是氣動肌肉在控制方面存在著下述的技術難點，其具有強非線性特性及時變特性，難以獲得精確的數學模型。而現有技術中存在著如下不足之處：第一，傳統的控制方法依賴于精確的數學模型，當氣動肌肉的負載和行程發生變化時，不能獲得較好的控制效果。第二，現有技術對氣動肌肉系統缺乏嚴格的穩定性分析，故難以從理論上保證系統的控制性能。第三，盡管現有技術中提出了諸如滑膜控制一類的控制方法，能夠適應系統特性的變化，但卻難以獲得較高的控制精度。因此如何尋找一種合適的控制策略以處理氣動肌肉系統的不確定性，并使其有效的應用于實際過程中，是亟待攻克的一大技術難關。

由此可見，現有技術存在控制效果差、控制性能差、控制精度低的技術問題。

技術實現要素：

針對現有技術的以上缺陷或改進需求，本發明提供了一種氣動肌肉的自適應控制方法和系統，其目的在于將實時位移和期望軌跡的期望位移輸入自適應控制器得到控制指令；將控制指令轉換為控制電壓，利用控制電壓控制氣動肌肉按照期望軌跡運行。由此解決現有技術存在控制效果差、控制性能差、控制精度低的技術問題。

為實現上述目的，按照本發明的一個方面，提供了一種氣動肌肉的自適應控制方法，包括：

(1)采集氣動肌肉運動時的實時位移，將實時位移和期望軌跡的期望位移輸入自適應控制器得到控制指令；

(2)將控制指令轉換為控制電壓，利用控制電壓控制氣動肌肉按照期望軌跡運行；

自適應控制器為：

其中，u是控制指令，是自適應變量，是自適應變量的變化率，是鎮定控制器，k1是自適應控制第一增益，k2是自適應控制第二增益，λ是自適應控制權重，ζ是期望軌跡的運動學參數，是根據期望位移計算的期望加速度，x1是實時位移，x2是根據實時位移計算的實時速度，r是期望位移，是根據期望位移計算的期望速度。

進一步的，自適應控制第一增益和自適應控制第二增益的范圍：

其中，π1是自適應控制第一邊界系數，bmax是單位質量的最大摩擦力系數，kmax是單位質量的最大彈力系數，π2是自適應控制第二邊界系數，d是在范圍內的任意常數，γmin是單位質量的最小收縮元力系數，αmax是單位質量的最大阻尼因子系數，是期望軌跡的最大速度，βmax是單位質量的最大彈簧因子系數，rmax是期望軌跡的最大位移，bmin是單位質量的最小摩擦力系數。

進一步的，單位質量的最大摩擦力系數、單位質量的最大彈力系數、單位質量的最小收縮元力系數、單位質量的最大阻尼因子系數、單位質量的最大彈簧因子系數和單位質量的最小摩擦力系數通過建立氣動肌肉的三元素模型，對氣動肌肉的三元素模型的參數進行辨識得到。

按照本發明的另一方面，提供了一種氣動肌肉的自適應控制系統，包括：

第一模塊，用于采集氣動肌肉運動時的實時位移，將實時位移和期望軌跡的期望位移輸入自適應控制器得到控制指令；

第二模塊，用于將控制指令轉換為控制電壓，利用控制電壓控制氣動肌肉按照期望軌跡運行；

自適應控制器為：

其中，u是控制指令，是自適應變量，是自適應變量的變化率，是鎮定控制器，k1是自適應控制第一增益，k2是自適應控制第二增益，λ是自適應控制權重，ζ是期望軌跡的運動學參數，是根據期望位移計算的期望加速度，x1是實時位移，x2是根據實時位移計算的實時速度，r是期望位移，是根據期望位移計算的期望速度。

進一步的，自適應控制第一增益和自適應控制第二增益的范圍：

其中，π1是自適應控制第一邊界系數，bmax是單位質量的最大摩擦力系數，kmax是單位質量的最大彈力系數，π2是自適應控制第二邊界系數，d是在范圍內的任意常數，γmin是單位質量的最小收縮元力系數，αmax是單位質量的最大阻尼因子系數，是期望軌跡的最大速度，βmax是單位質量的最大彈簧因子系數，rmax是期望軌跡的最大位移，bmin是單位質量的最小摩擦力系數。

進一步的，單位質量的最大摩擦力系數、單位質量的最大彈力系數、單位質量的最小收縮元力系數、單位質量的最大阻尼因子系數、單位質量的最大彈簧因子系數和單位質量的最小摩擦力系數通過建立氣動肌肉的三元素模型，對氣動肌肉的三元素模型的參數進行辨識得到。

總體而言，通過本發明所構思的以上技術方案與現有技術相比，能夠取得下列有益效果：

(1)本發明將實時位移和期望軌跡的期望位移輸入自適應控制器得到控制指令；將控制指令轉換為控制電壓，利用控制電壓控制氣動肌肉按照期望軌跡運行。本發明設計的自適應控制器，可以在氣動肌肉系統參數存在強的時變性和不確定性的情況下，在線自適應地估計參數，使氣動肌肉系統能夠主動適應時變性和不確定性，進而改善控制效果、提升控制性能、提高控制精度。

(2)優選的，本發明限制自適應控制第一增益和自適應控制第二增益的范圍，在改善控制效果、提升控制性能、提高控制精度的同時保證了氣動肌肉的穩定性。

(3)優選的，本發明通過建立氣動肌肉的三元素模型，對氣動肌肉的三元素模型的參數進行辨識，進而優化對自適應變量的估計。

附圖說明

圖1是本發明實施例提供的一種氣動肌肉控制系統的實驗平臺結構圖；

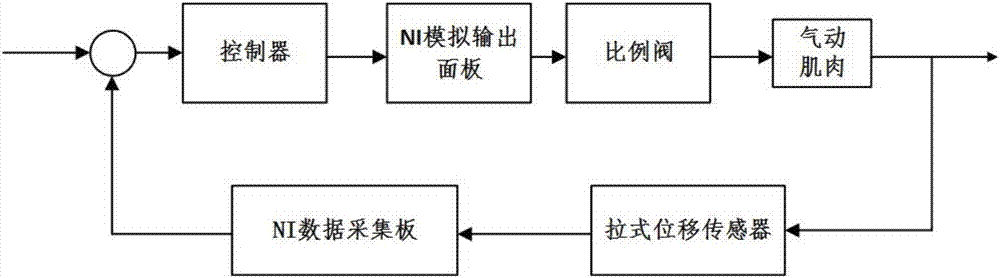
圖2是本發明實施例提供的氣動肌肉控制原理框圖；

圖3是本發明實施例提供的一種氣動肌肉的自適應控制方法的流程圖；

圖4是本發明實施例中的彈力系數的辨識結果圖；

圖5是本發明實施例中的收縮元力系數的辨識結果圖；

圖6是本發明實施例氣動肌肉充氣狀態下的摩擦力系數的辨識結果圖；

圖7是本發明實施例氣動肌肉放氣狀態下的摩擦力系數的辨識結果圖；

圖8是本發明實施例仿真中自適應控制器、非自適應控制器、pid控制器的跟蹤性能在0-12s的比較示意圖；

圖9是本發明實施例仿真中自適應控制器、非自適應控制器、pid控制器的跟蹤性能在52-68s的比較示意圖；

圖10是本發明實施例實驗中自適應控制器、非自適應控制器、pid控制器的低頻跟蹤性能在0-12s的比較示意圖；

圖11是本發明實施例實驗中自適應控制器、非自適應控制器、pid控制器的低頻跟蹤性能在52-68s的比較示意圖；

圖12是本發明實施例實驗中自適應控制器、非自適應控制器、pid控制器的高頻跟蹤性能比較示意圖。

具體實施方式

為了使本發明的目的、技術方案及優點更加清楚明白，以下結合附圖及實施例，對本發明進行進一步詳細說明。應當理解，此處所描述的具體實施例僅僅用以解釋本發明，并不用于限定本發明。此外，下面所描述的本發明各個實施方式中所涉及到的技術特征只要彼此之間未構成沖突就可以相互組合。

本發明首先提供了一種氣動肌肉控制系統的實驗平臺，如圖1所示，其組成部分有：拉線位移傳感器1、負載2、氣動肌肉3、空氣壓縮機4、比例閥5、ni控制器6、直流電源7、顯示器8。該平臺采用festo公司生產的氣動肌肉festomaxm-20-aa，其一端固定在平臺的支架上，而另一端為活動端，與負載2相連。氣動肌肉充氣時直徑增大，長度減小；反之放氣時直徑減小，長度增加。空氣壓縮機4提供整個系統的氣壓輸入，通過比例閥5的調節，可以控制實際輸入到氣動肌肉3中的氣壓量。拉線位移傳感器1用于測量氣動肌肉3活動端的位移，ni控制器6通過數據采集卡的模數轉換模塊采集位移信號，控制器利用得到的反饋信號，根據自適應伺服控制算法計算出控制量，再通過采集卡的數模轉換模塊輸出實際控制電壓給比例閥5，由比例閥5輸出氣壓控制氣動肌肉的動作。

對于上述氣動肌肉3的控制原理框圖如圖2所示，控制器發出電壓信號通過ni模擬輸出面板輸出至比例閥，從而調節進入到氣動肌肉的氣壓進而改變氣動肌肉的收縮量，氣動肌肉的收縮量即活動端的位移通過拉線位移傳感器反饋到ni數據采集板，將反饋量與給定輸入量進行比較，不斷修正偏差而實現對給定輸入的跟蹤。

上述的ni控制器6的信號采集及激勵信號的產生是基于labview的開發環境，labview是實驗室虛擬儀器集成環境的簡稱，也是目前應用最廣、發展最快、功能最強的圖形化軟件開發集成環境。使用labview編程就如同堆積木一樣簡單，既使沒有編程經驗的人也可以在很短的時間內編制出界面美觀、功能強大的自動化程序。程序員無需知道每個圖標的內部結構，只需知道其具體功能，并按照一定的邏輯順序將它們用線連接起來，就能完成一路模擬量數據采集的任務。

ni模擬輸出面板使用了ni控制器6的模擬輸出功能，ni數據采集板使用了ni控制器6的數據采集功能。

建立三元素模型：

其中，ys，分別代表氣動肌肉的位移，速度，加速度，p代表氣動肌肉的內部氣壓，m是氣動肌肉的質量，g是重力加速度，式中的非線性項k(p)ys及f(p)分別是摩擦力，彈力及收縮元力，令ys＝0對應于氣動肌肉完全放氣和伸展的狀態，則當氣動肌肉收縮時，ys增加。摩擦力系數b(p)，彈力系數k(p)，收縮元力系數f(p)具有如下的表達形式：

b(p)＝α0-α1p

k(p)＝β0-β1p

f(p)＝γ0+γ1p

式中，α0為氣動肌肉的阻尼因子第一系數，α1為氣動肌肉的阻尼因子第二系數，β0為氣動肌肉的彈簧因子第一系數，β1為氣動肌肉的彈簧因子第二系數，γ0為氣動肌肉的收縮力因子第一系數，γ1為氣動肌肉的收縮力因子第二系數。

預設一個氣壓值p0，設置氣動肌肉平衡點ys＝y0，根據平衡條件，有f(p0)-k(p0)ys＝mg；

以設定的平衡點作為基準，令控制指令u＝δp＝p-p0，實時位移y＝ys-y0，為實時加速度，為實時速度，α為單位質量的阻尼因子系數，β為單位質量的彈簧因子系數，γ為單位質量的收縮元力系數，b為單位質

量的摩擦力系數，k為單位質量的彈力系數，重構三元素模型：

b＝(α0-α1p0)/m，k＝(β0-β1p0)/m，α＝α1/m，β＝β1/m，γ＝(γ1+β1y0)/m；

對于重構的三元素模型，令第一狀態變量x1＝y，x＝[x1，x2]^t，為第一狀態變量的變化率，為第二狀態變量的變化率，建立三元素模型的狀態空間表達式如下：

對步驟狀態空間表達式進行坐標變換則誤差的動力學模型為：r為期望位移，為期望速度，為期望加速度，

我們期望氣動肌肉能夠跟蹤給定的期望軌跡，這一條件可描述為：y(t)表示t時刻的實時位移，r(t)表示t時刻的期望位移。

可從狀態空間表達式中解出所需控制輸入，即

對u進行線性化：

u＝μ^tζ+o(ζ^[2])

其中，μ為線性化系數，μ＝[μ1，μ2，μ3]^t，ζ為期望軌跡的運動學參數，o(ζ^[2])是ζ的二階無窮小，取

根據u線性化后的結構，設計自適應控制器如下：

其中，是自適應變量，代表對μ的估計，是自適應變量的變化率，是鎮定控制器，k1是自適應控制第一增益，k2是自適應控制第二增益，λ是自適應控制權重。

如圖3所示，一種氣動肌肉的自適應控制方法，包括：

(1)采集氣動肌肉運動時的實時位移，將實時位移和期望軌跡的期望位移輸入自適應控制器得到控制指令；

(2)將控制指令轉換為控制電壓，利用控制電壓控制氣動肌肉按照期望軌跡運行；

自適應控制器為：

其中，u是控制指令，是自適應變量，是自適應變量的變化率，是鎮定控制器，k1是自適應控制第一增益，k2是自適應控制第二增益，λ是自適應控制權重，ζ是期望軌跡的運動學參數，是根據期望位移計算的期望加速度，x1是實時位移，x2是根據實時位移計算的實時速度，r是期望位移，是根據期望位移計算的期望速度。

進一步的，自適應控制第一增益和自適應控制第二增益的范圍：

其中，π1是自適應控制第一邊界系數，bmax是單位質量的最大摩擦力系數，kmax是單位質量的最大彈力系數，π2是自適應控制第二邊界系數，d是在范圍內的任意常數，γmin是單位質量的最小收縮元力系數，αmax是單位質量的最大阻尼因子系數，是期望軌跡的最大速度，βmax是單位質量的最大彈簧因子系數，rmax是期望軌跡的最大位移，bmin是單位質量的最小摩擦力系數。

進一步的，單位質量的最大摩擦力系數、單位質量的最大彈力系數、單位質量的最小收縮元力系數、單位質量的最大阻尼因子系數、單位質量的最大彈簧因子系數和單位質量的最小摩擦力系數通過建立氣動肌肉的三元素模型，對氣動肌肉的三元素模型的參數進行辨識得到。

進一步的，為了比較自適應伺服控制算法與其他控制算法的性能，本發明還對上述三元素模型中的系統參數進行了辨識。如圖4所示，k(p)與p之間呈近似分段線性關系，如圖5所示，f(p)與p之間呈近似線性關系。而對摩擦力系數b(p)的辨識需要在動態過程中進行，值得注意的是，b(p)與p之間并不是簡單的線性關系，并且對于相同的氣壓p，不同負載對應著不同的摩擦力系數b(p)，這意味著摩擦力系數b(p)不是簡單地與氣壓p相關，可能存在著更為復雜的函數關系。但考慮到總體來說，摩擦力系數的值較小，最終依然采用了一條擬合的直線和其可能產生的誤差邊界來描述b(p)與p之間的關系。b(p)與p之間的關系如圖6和圖7所示，由圖可見，b(p)與p的關系與氣動肌肉處于充氣狀態還是放氣狀態有關。從辯識過程可知氣動肌肉系統參數的不確定性和強非線性。

接著，氣動肌肉系統參數的不確定性范圍計算如下：

713≤b≤1024

5.2×10³≤k≤6.1×10³

6.44×10^-5≤|α|≤9.1×10^-4

0≤|β|≤0.061

5.38×10^-4≤γ≤0.0024

b的單位是k的單位是α的單位是β的單位是γ的單位是根據上述不確定性計算結果，在其取值范圍內任意選擇數值作為系統參數來設計傳統的控制器，用于比較。

我們分別通過仿真和實驗驗證本發明中的自適應控制器對給定正弦輸入信號的跟蹤能力，并將自適應控制器adaptive與傳統pid控制器，其他非自適應控制器non-adaptive進行了比較，圖8是本發明實施例仿真中自適應控制器、非自適應控制器、pid控制器的跟蹤性能在0-12s的比較示意圖；圖9是本發明實施例仿真中自適應控制器、非自適應控制器、pid控制器的跟蹤性能在52-68s的比較示意圖；在仿真中，自適應控制器的跟蹤誤差為0.03mm，而pid控制器和非自適應控制器的跟蹤誤差分別為0.75mm，0.013mm。圖10是本發明實施例實驗中自適應控制器、非自適應控制器、pid控制器的低頻跟蹤性能在0-12s的比較示意圖；圖11是本發明實施例實驗中自適應控制器、非自適應控制器、pid控制器的低頻跟蹤性能在52-68s的比較示意圖；圖12是本發明實施例實驗中自適應控制器、非自適應控制器、pid控制器的高頻跟蹤性能比較示意圖。在實驗中做了更為細致的比較，分別比較了三種控制器對低頻信號和高頻信號的跟蹤能力。仿真和實驗結果均表明，自適應控制器的跟蹤能力優于其他兩種控制器。

本領域的技術人員容易理解，以上所述僅為本發明的較佳實施例而已，并不用以限制本發明，凡在本發明的精神和原則之內所作的任何修改、等同替換和改進等，均應包含在本發明的保護范圍之內。