本發明涉及再入滑翔飛行器軌跡預測，具體為一種基于最小代價準則的再入滑翔飛行器軌跡預測方法。

背景技術：

1、再入滑翔飛行器作為一種全球快速打擊武器，在臨近空間的長時間飛行具有速度快、突防能力強和打擊范圍廣的特點，，同時，對防御方的預警、探測、跟蹤和攔截提出了新的挑戰，因此針對再入滑翔目標的軌跡預測研究具有重要意義。

2、和彈道目標不同，再入滑翔目標再入滑翔時會進行大范圍的高速機動，防御方在獲取目標軌跡信息后，為降低攔截彈的機動過載、提高防御武器的作戰效能，通常采用基于預測命中點的零控攔截策略，這對再入滑翔目標的軌跡預測精度和預測時長提出了很高要求。

3、從預測機制上，針對再入滑翔目標的軌跡預測技術主要分為基于數據分析和基于模型兩大類軌跡預測方法。第一種方法通過分析目標軌跡的歷史跟蹤數據來進行預測，具有短期預測精度高、方法實現簡單的特點。楊春偉等借助注意力機制和lstm(long?shortterm?memory)結構，將目標的狀態信息和攻角作為輸入，實現了一種seq2seq的軌跡預測方法；韓春耀等運用先分解再集成的預測思路，通過對目標軌跡序列的趨勢項、周期項和隨機項分別進行預測，實現了對目標高精度的短期預測；胡星志等通過高斯過程回歸對目標的運動軌跡進行統計學分析，對具有同數據分布的目標軌跡預測效果較好，但缺乏目標運動模型支撐，軌跡預測的約束性不強。上述方法直接對目標的淺層信息進行處理，缺乏深層的模型約束，難以滿足高精度、中長期的軌跡預測需求。

4、此外，第二種方法從預測機理上主要分為參數估計、模式辨識和意圖推斷三種類型。其中，參數估計把再入滑翔目標看作非合作目標，將目標質量、受力面積、氣動系數等未知信息整合為一個參數，借助動力學模型實現對目標的迭代預測。在先驗信息不足的情況下，確定合適且易于預測的參數是該方法的關鍵。王路等通過對目標的升阻比進行估計來實現軌跡預測，在升阻比呈線性變化時預測效果較好；翟岱亮等給出了一組在高空高速環境下和目標姿態近似線性的氣動參數，并結合最小二乘擬合實現了對再入滑翔目標的長時軌跡預測；李世杰等在文獻的基礎上，構造了一組適用于軌跡預測的控制變量，實現了對目標不同機動模式下軌跡的預測；李明杰等分別將控制參數和氣動參數同lstm網絡結合，仿真表明控制參數在再入目標軌跡預測中具備優越性。上述方法僅通過參數估計對目標軌跡進行預測，適用于參數變化規律簡單的情形，存在很大的局限性。然而，目標在再入過程中，會以特定的機動模式進行突防或者根據預先確定的攻擊意圖來實時改變運動規律，此時參數估計的方法便不再適用。基于此，諸多學者對基于再入滑翔飛行器模式辨識和意圖推斷的軌跡預測方法進行了十分有益的探索。

5、在目標機動模式辨識方面，根據不同的機動模式預先建立相應的預測模型，然后通過識別技術進行模型匹配，已被證實是切實可行的方向。陳南華等利用歷史跟蹤數據確定自回歸集成滑動平均(autoregressive?integrated?moving?average，arima)模型的參數，結合ukf算法實現對目標軌跡的預測；魏喜慶等針對具有周期跳躍特點的再入目標軌跡，利用雙正弦和函數匹配目標運動規律，遞推得到目標預測軌跡；程云鵬等根據機動模式的定義，生成機動模式集用來訓練svm，實現了對目標機動軌跡的模式識別和預測；sun等針對簡化條件下的目標縱向跳躍滑翔彈道，用線性衰減項和幅度衰減正弦項組成了高度和速度等變量的解析表達式，借助lstm網絡實現了軌跡預測管道的計算。在目標意圖推斷方面，由于其再入制導總是具備一定的目的性，通過引入攻擊意圖，對機動模式辨識方法的預測結果進行修正，可進一步提高軌跡預測精度。張凱等通過構造意圖代價函數，推導了機動模式和運動狀態的遞推公式，實現了目標機動不確定條件下的軌跡預測。hu等針對機動模式突變的問題，在文獻的基礎上，通過意圖代價函數和貝葉斯原理將軌跡預測問題轉化為求解可達區內目標可能經過區域的概率，算法不依賴目標動力學過程，短期預測精度較高，但耗時較長，不利于在線預測；李佳麗等在文獻的基礎上，對意圖代價函數進行了改進，并分別構建了縱向和側向的時變預測模型集，實現了再入滑翔目標的多模型多意圖融合軌跡預測，但代價系數需人為給定，算法不具備普適性；xu等文獻通過深度神經網絡建立了目標初始狀態、控制量和飛行區域的關系，提高了對目標攻擊意圖推斷和軌跡預測的計算效率，但算法并未考慮禁飛區的存在對目標軌跡的影響。

6、所以我們提出了一種基于最小代價準則的再入滑翔飛行器軌跡預測方法，以便于解決上述中提出的問題。

技術實現思路

1、本發明的目的在于提供一種基于最小代價準則的再入滑翔飛行器軌跡預測方法，以解決上述背景技術提出的目前市場上的問題。

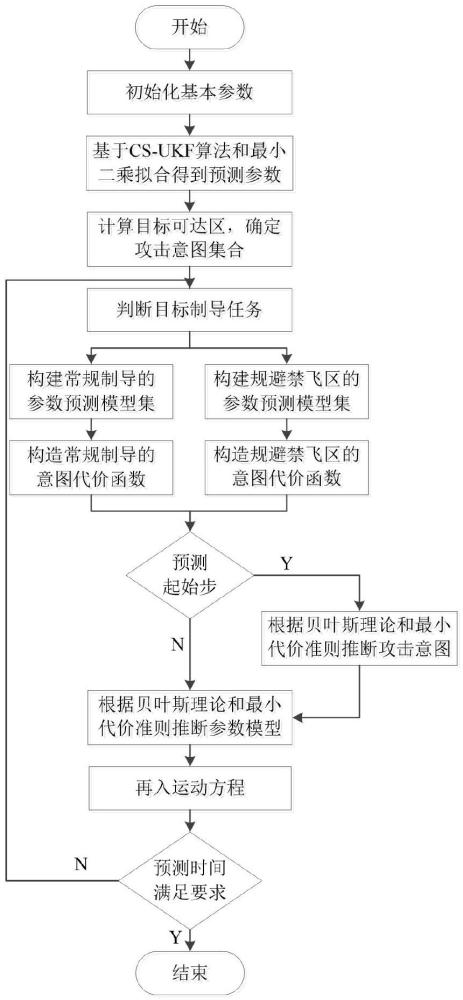
2、為實現上述目的，本發明提供如下技術方案：一種基于最小代價準則的再入滑翔飛行器軌跡預測方法，包括如下步驟：

3、step1：初始化雷達參數、預測參數、禁飛區和意圖位置信息；

4、step2：根據cs-ukf濾波算法對目標進行跟蹤，得到控制參數利用最小二乘法擬合得到預測的

5、step3：計算目標可達區，確定攻擊意圖集合θ，對每個可能攻擊的意圖執行step4～step6；

6、step4：判斷目標制導任務，當目標任務為τf時，轉入step5；當目標任務為τb時，轉入step6；

7、目標制導任務的判斷包括：

8、根據禁飛區是否影響目標軌跡將制導任務分為規避禁飛區和常規制導，分別記為τb和τf，判斷邏輯由角度條件和距離條件組成，如圖2所示，具體形式如下：

9、

10、式中：ψ∈(ψbmin,ψbmax)是角度條件，表明此時目標的速度指向禁飛區，ψbmin表示目標到禁飛區邊界的最小航跡偏角，ψbmax表示目標到禁飛區邊界的最大航跡偏角；是距離條件，表明目標以當前傾側角或者變號后的傾側角繼續飛行會與禁飛區相交，即禁飛區影響了目標的正常軌跡，γσ、γ-σ分別表示傾側角符號為正號和負號的瞬時轉彎圓的邊，γb表示禁飛區的邊；

11、其中，ψbmin和ψbmax的表達式如下：

12、

13、式中：ψb是目標到禁飛區中心的航跡偏角，rb是禁飛區的半徑，sb為目標到禁飛區圓心的剩余航程；剩余航程sb由下式確定：

14、

15、式中：為禁飛區圓心的經緯度；ψb的計算公式如下：

16、

17、當目標瞬時轉彎圓和禁飛區相交時，存在下式特點：

18、stb＜rturn+rb?(10)

19、式中：rturn為瞬時轉彎半徑，rb為禁飛區半徑，stb為瞬時轉彎圓和禁飛區的圓心距；其中，瞬時轉彎半徑rturn由下式確定：

20、

21、瞬時轉彎圓和禁飛區的圓心距可由下式確定：

22、

23、式中：為飛行器瞬時轉彎圓的圓心經緯度，計算公式如下：

24、

25、根據式(6)判斷出目標的制導任務后，對不同的制導任務的需求，構建不同的預測模型集。

26、step5：構建常規制導的參數預測模型集λ，并構造常規制導的意圖代價函數if，計算相應的代價；

27、構建常規制導的參數預測模型集包括：

28、1)縱向參數預測模型集

29、對再入滑翔目標縱向預測時，使用最小二乘法對跟蹤段的濾波參數進行函數擬合得到進而得到未來時刻的參數預測值為方便描述，令μ＝[kd,σ,kl]，假設參數濾波值滿足以真實值為均值的高斯分布，參數預測值滿足以預測結果為均值的高斯分布，參數分布如下所示：

30、

31、式中：為未來時刻參數預測值可能的取值，和分別為me和mm的標準差；

32、當由式(6)判斷為目標執行制導任務τf，構建縱向參數預測模型集時，從mm～n(mp,(σp)2)分布中各抽取n個參數，構成n3個模型集；為提高軌跡預測精度，模型集的范圍應盡可能的覆蓋真實值，同時模型集的個數盡可能的少，以縮減算法的求解時間；由于預測段參數的分布情況未知，無法直接確定σp的取值，因此通過對參數濾波值me的標準差σe放縮得到σp，即

33、σp＝λσe?????????????????????????????????????????????????????(15)

34、由于參數跟蹤時，參數真實值m是未知的，假設函數擬合的結果和真實值比較接近，即參數濾波值也滿足以擬合結果為均值的高斯分布

35、me～n(mf,(σf)2)?????????????????????????????????????????????(16)

36、

37、式中：為me的標準差；

38、假設不同時刻的參數濾波值服從的高斯分布的方差相同，由標準差的定義可知：

39、

40、式中：ne為跟蹤段的總步長；

41、由式(14)進行參數采樣時，參數mm由下式確定：

42、

43、2)側向參數預測模型集

44、當目標進行常規制導時，利用航跡偏差角走廊來確定目標當前時刻的傾側角符號，由此組成側向參數預測模型集；和傳統的航跡偏差角走廊不同的是，由于禁飛區可能會擠占走廊寬度，導致傾側角的符號發生反復偏轉，為避免這一現象，建立走廊時需要加入一定的補償；帶補償的航跡偏差角走廊的示意圖如3所示；

45、對航跡偏差角走廊進行補償時，根據目標與禁飛區的相對位置關系決定航跡偏角的上下界；當ψ≥ψbmax時，可得：

46、

47、當ψ≤ψbmin時，可得：

48、

49、式中：δψfed表示目標原先的航跡偏差角走廊范圍；

50、根據補償后的航跡偏差角走廊確定目標的傾側角符號：

51、

52、式中：ψf表示目標到攻擊意圖的航跡偏角；

53、結合目標縱向參數模型集，最終確定n3個預測模型集，即λ＝{μ1,m2,…mn}，其中

54、當目標任務為τf時，構造意圖代價函數if主要考慮角度代價和能量代價，具體形式如下：

55、

56、式中：max(|δψf|-δψfed,0)為角度代價，|δψf|＝|ψ-ψf|表示目標的航跡偏角和到攻擊意圖的航跡偏角的差的絕對值，當|δψf|≤δψfed時，角度代價統一為0，當|δψf|＞δψfed時，角度代價為|δψf|-δψfed，意圖代價函數傾向于選擇使得|δψf|減小的參數預測模型m；|sref-sf|為能量代價，sref表示目標在當前參數預測模型下的速度降到規劃速度vref時的航程，sf表示目標到攻擊意圖的剩余航程，當sf＝sref時，能量代價為0，當sf≠sref時，sf和sref相差越大，能量代價越大，意圖代價函數傾向于選擇使得sf接近sref的參數預測模型m；

57、剩余航程sf由下式確定：

58、

59、式中：為攻擊意圖的經緯度。

60、由于目標根據參數預測模型m通過積分計算sref耗時過大，不適合防御方快速進行模式推斷；為提高預測速度，便于衡量不同參數預測模型的意圖代價，將目標平衡滑翔條件下的sr′ef來代替實際的sref進行比較，忽略目標縱向實際運動帶來的航程偏差；根據目標平衡滑翔條件下的射程和速度的關系，確定sr′ef的計算公式為：

61、

62、式中：v0為目標當前的速度，表示目標的升阻比。

63、step6：構建規避禁飛區的參數預測模型集λ，并構造規避禁飛區的意圖代價函數ib，計算相應的代價；

64、構建規避禁飛區的參數預測模型集包括：

65、1)縱向預測模型集

66、當目標執行規避禁飛區的制導任務時，存在兩種當前的轉彎能力不足以完全規避禁飛區的情況；第一種，當ψ和ψf在ψb的兩側時，存在目標的瞬時轉彎圓和禁飛區相交，需要繞過禁飛區才能實現規避；第二種，當ψ和ψf在ψb的一側，同時在sign(σ)＝sign(ψ-ψb)時的瞬時轉彎圓和禁飛區相交，禁飛區的一小部分阻擋了目標的制導軌跡；兩種情況的示意圖如圖4和圖5所示；

67、此時，需要適當的增大傾側角的幅值，以提高轉彎能力；在常規制導的參數預測模型集的縱向參數預測模型集的基礎上，將傾側角幅值|σp|的取值盡可能的覆蓋其定義域[0,π/2]，具體過程如下：

68、在[0,π/2]范圍內，等距采樣n個點，并按照式(14)可得每個采樣點的權重

69、

70、對采樣點的權重進行歸一化

71、

72、實際采樣時，在[0,1]內產生一個隨機數δ′，和n個點的權重進行比較，插值得到新的采樣點|σm|；

73、2)側向參數預測模型集

74、側向預測時，由于目標、禁飛區和攻擊意圖的相對位置關系存在多種情況，目標規避禁飛區的同時要考慮對到達攻擊意圖的常規制導任務的影響，綜合自身的機動能力、能量損失和任務完成情況才能做出最小代價的側向機動模式；因此側向參數預測模型集考慮傾側角符號的兩種情況{1,-1}，最終側向機動模式由意圖代價函數輔助推斷；

75、結合目標縱向參數模型集，最終確定2n3個預測模型集，即λ＝{m1,m2,…m2n}，其中

76、當目標任務為τb時，由于此時規避禁飛區是首要任務，但同時要考慮對最終制導任務的影響最小，因此構造意圖代價函數ib時不考慮能量代價，主要考慮規避角度代價和制導角度代價；具體形式如下：

77、ib＝ε1δψb+ε2δψbf?(28)

78、式中：ε1δψb是規避角度代價，ε1為規避代價系數；ε2δψbf是制導角度代價，ε2為制導代價系數；

79、1)規避角度代價

80、在規避角度代價中，δψb越大，規避角度代價越大；由于目標的轉彎能力有限，因此需要對在參數預測模型m中的傾側角控制下的目標規避禁飛區情況進行定量描述，選擇規避代價最小的參數預測模型；δψb由下式決定：

81、

82、計算規避代價系數時，需要考慮ψ、ψb和ψf的關系；在目標可規避禁飛區的傾側角幅值集合中，當軌跡和禁飛區相切時，損耗的能量最少；因此，規避代價系數定義如下：

83、

84、式中：σtan為目標瞬時轉彎圓和禁飛區外切時所需的傾側角，σ′為上一時刻的傾側角幅值，當|σ|＝σtan時，規避代價系數為1，當|σ|≠σtan，|σ|與σtan偏差越大，規避代價系數越大，意圖代價函數傾向于選擇目標瞬時轉彎圓和禁飛區外切時的|σ|；σtan具體計算過程如下：

85、由目標瞬時轉彎圓和禁飛區外切關系可得

86、stb＝rturn+rb?????(31)

87、由式(12)和(13)可得

88、

89、上式展開可得

90、

91、整理成瞬時轉彎半徑的表達式

92、

93、聯立式(11)和(34)可得

94、

95、2)制導角度代價

96、在制導角度代價中，δψbf的定義如下：

97、

98、當ψbmin≤ψf≤ψbmax時，相對目標而言，攻擊意圖在禁飛區后側，目標無論朝哪個方向規避，sign(δψbf)都為1，即目標規避禁飛區的同時，會增大制導代價；當ψf＞ψbmax或ψf＜ψbmin時，相對目標而言，攻擊意圖在禁飛區一側，目標朝攻擊意圖方向規避，會產生較小的制導代價，否則，將產生較大的制導代價；

99、制導代價系數ε2定義如下

100、

101、當sb＜sf/2時，ε2＜0.5，表示目標離攻擊要地較遠，對于規避禁飛區而言，制導任務的影響占比較小，此時制導代價較小；當sb≥sf/2時，ε2≥0.5，表示目標離攻擊要地較近，規避禁飛區將直接影響目標最終制導任務的完成情況，因此制導代價較大；

102、當存在多個禁飛區影響目標軌跡時，選擇距離最近的禁飛區作為主禁飛區，用以表征綜合規避禁飛區的意圖代價，即：

103、

104、式中：nb為影響目標軌跡的禁飛區的個數。

105、step7：推斷代價最小的攻擊意圖ηt；

106、對攻擊意圖ηt的后驗概率進行推導；

107、

108、同理，將狀態量拆成兩部分，可得：

109、

110、式中，p(xk|x1:k-1,ηt)為上文式(44)所求的意圖ηt的似然概率，p(ηt|x1:k-1)為上一時刻的意圖ηt的后驗概率，p(xk|x1:k-1)為目標一步預測的條件概率，計算公式如下：

111、

112、由貝葉斯定理可得的后驗概率為：

113、

114、因此，意圖ηt的后驗概率為：

115、

116、根據式(52)和最小代價準則，目標最有可能的攻擊意圖為：

117、

118、step8：推斷代價最小的參數預測模型mn，根據重構后的目標運動方程組進行迭代積分，得到預測的目標位置；

119、當目標的攻擊意圖為ηt時，根據意圖代價函數確定在參數預測模型mn下狀態轉移的似然概率，

120、

121、其中，

122、根據貝葉斯定理，參數模型mn的后驗概率為：

123、

124、在對等號右邊的分式進行處理時，將狀態量拆成兩部分，表達成似然概率乘以先驗概率的形式：

125、

126、分子分母上的兩個先驗概率相結合形成上一時刻參數模型mn的后驗概率：

127、

128、由于狀態轉移的過程具有馬爾科夫性，對參數模型mn下的狀態轉移進行簡化，可得到：

129、

130、式中：p(xk|xk-1,mn,ηt)為參數模型mn的似然概率，已經由意圖代價函數確定，p(mn|x1:k-1,ηt)為上一時刻參數模型mn的后驗概率，p(xk|x1:k-1,ηt)表示意圖ηt的似然概率，計算公式如下：

131、

132、由貝葉斯定理可得的后驗概率為：

133、

134、因此，參數模型mn的后驗概率如下：

135、

136、根據式(46)和最小代價準則，目標在攻擊意圖ηt下最有可能的參數預測模型為：

137、

138、step9：當預測時間到達規劃時間后，結束預測，否則循環執行step4～step6和step8。

139、與現有技術相比，本發明的有益效果是：

140、(1)本發明通過劃分目標制導任務，構建任務匹配的時變參數預測模型集，減少了側向參數模型的冗余，保證了預測算法的快速實現；綜合考慮目標的機動能力、制導意圖和戰場態勢，提出了一種具備自適應代價系數的意圖代價函數，提高了制導意圖代價估計的準確性；基于貝葉斯理論和最小代價準則推斷了目標的攻擊意圖和參數模型，減少了預測過程中的誤差累積。

141、(2)本發明仿真實驗結果表明，在多種情況下，本發明所提預測方法能夠實現對目標攻擊意圖的準確推斷和位置的準確預測，和已有方法相比，具有預測精度高和算法耗時短的優勢。

142、上述概述僅僅是為了說明書的目的，并不意圖以任何方式進行限制。除上述描述的示意性的方面、實施方式和特征之外，通過參考附圖和以下的詳細描述，本發明進一步的方面、實施方式和特征將會是容易明白的。