本發明涉及人工智能領域，尤其涉及一種人工智能模型加速訓練推理方法及裝置。

背景技術：

1、隨著互聯網、大數據、云計算等技術的飛速發展，人工智能獲得了前所未有的數據資源和計算能力。機器學習、深度學習、強化學習、遷移學習等人工智能關鍵技術的突破，使得人工智能在語音識別、圖像識別、自然語言處理等領域取得了重大進展。這種進步不僅體現在理論上的重大突破，也在多個產業領域中實現了實際應用，人工智能模型的應用已經逐漸滲透到醫療、交通、金融、教育、制造等多個領域。然而在實際應用中，除了需要考慮模型本身的應用效果，還需要考慮模型應用的成本，成本主要來自于存儲資源和計算資源的占用。在人工智能模型中需要存儲大量的矩陣和進行大量的矩陣運算，尤其是在處理大規模數據應用時，矩陣的維度較大，部署占用的高存儲和矩陣運算的高計算復雜度都會大大增加模型在訓練和推理過程中的資源使用，進而增加應用成本。

技術實現思路

1、針對人工智能模型在推廣應用時面臨的急需降低訓練和推理過程中占用資源成本的需求，本發明提供了一種人工智能模型加速訓練推理方法，利用多層矩陣低秩壓縮技術對人工智能模型中的協方差矩陣、權重矩陣等大維度矩陣進行壓縮、分解和轉化，最終將矩陣表示為多個塊對角矩陣相乘，分別存儲各個塊對角矩陣以減少存儲資源占用，并且實現模型訓練推理過程中矩陣求逆運算的計算復雜度降低和高度并行化，降低模型使用的算力門檻。

2、本發明的技術方案是：

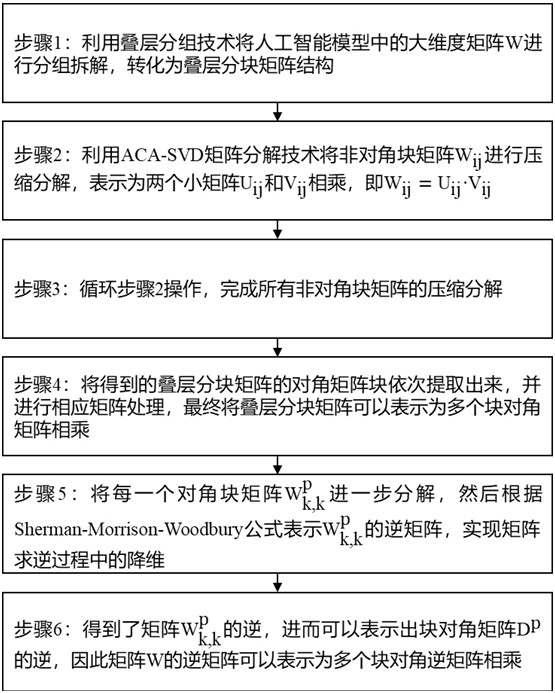
3、一種人工智能模型加速訓練推理方法，包括如下步驟：

4、s1.利用疊層分組技術將人工智能模型中的大維度矩陣w進行分組拆解，轉化為疊層分塊矩陣結構。

5、s2.利用aca-svd矩陣分解技術將非對角塊矩陣進行壓縮分解，表示為兩個小矩陣和相乘，即，其中i和j分別表示非對角塊矩陣所在層的相互作用組的組號，也是對應所在層矩陣塊的行列號。

6、s3.循環步驟s2操作，完成所有非對角塊矩陣的壓縮分解。

7、s4.將壓縮分解后得到的疊層分塊矩陣的對角矩陣塊依次提取出來，并進行相應矩陣處理，最終將疊層分塊矩陣表示為多個塊對角矩陣相乘。

8、s5.將每一個對角塊矩陣進一步分解，然后根據sherman-morrison-woodbury公式表示的逆矩陣，實現矩陣求逆過程中的降維。

9、s6.得到了矩陣的逆，進而可以表示出塊對角矩陣的逆，因此矩陣w的逆矩陣可以表示為多個塊對角逆矩陣相乘。

10、進一步的，所述步驟s1中，利用疊層分組技術將人工智能模型中的大維度矩陣w進行分組拆解，轉化為疊層分塊矩陣結構的具體步驟為：

11、s1.1.?設置分組拆解過程中最小矩陣塊維度閾值為min_n。

12、s1.2.?將矩陣w分別進行維度均等的行分割和列分割，得到第一層分組矩陣，判斷每個矩陣塊的維度是否小于維度閾值min_n，若小于則停止操作，否則進行下一步。

13、s1.3.?將上一層分組矩陣的對角塊進行維度均等的行分割和列分割，得到下一層分組矩陣，判斷每個矩陣塊的維度是否小于維度閾值min_n，若小于則停止操作，否則進行下一步。

14、s1.4.?重復步驟s1.3，直到最小矩陣塊維度小于維度閾值min_n，停止操作，以獲得2層矩陣為例，對應的矩陣w則變為：

15、，

16、公式中上標表示層號，下標表示在相應層相互作用組的組號。

17、進一步的，所述步驟s2中，利用aca-svd矩陣分解技術將非對角塊矩陣進行壓縮分解的具體步驟為：

18、s2.1.?采用aca算法對矩陣進行壓縮，在壓縮過程中需要對aca算法設置一個容許精度(e)，可以使矩陣分解為兩個維度較小的矩陣和。

19、s2.2.?將矩陣和的轉置矩陣分別用qr分解技術進行分解，得到：

20、，

21、，

22、因此矩陣可以表示為：

23、，

24、p表示的是層號，k表示的是相應層的組號。

25、進一步的，所述步驟s5中，將每一個對角塊矩陣進一步分解的具體特征為：將每一個對角塊矩陣進一步分解為：

26、，

27、進一步的可以表示為：。

28、進一步的，所述步驟s5中，根據sherman-morrison-woodbury公式表示的逆矩陣，實現矩陣求逆過程中的降維，具體特征為：將的逆矩陣可以表示為：

29、，

30、其中

31、，

32、矩陣的維度為非對角塊矩陣的秩，其值要遠小于的維度，實現了矩陣求逆過程中的降維。

33、進一步的，所述步驟s6中，矩陣w的逆矩陣可以表示為多個塊對角逆矩陣相乘的具體特征為：矩陣w的逆矩陣可以表示為：

34、，

35、其中l表示疊層矩陣總的層數。其中每個塊對角矩陣中的各個對角塊矩陣都是相對獨立的，在矩陣運算過程中不存在遞歸關系，可以實現高度并行運算。

36、此外，本發明還提供了一種人工智能模型加速訓練推理裝置，用于實現上述所述的方法，包括：矩陣疊層分組模塊、aca-svd矩陣分解模塊、矩陣處理存儲模塊、模型訓練模塊、模型推理模塊。

37、其中，

38、矩陣疊層分組模塊，用于按照步驟s1中過程實現將人工智能模型中的大維度矩陣w進行分組拆解，轉化為疊層分塊矩陣結構。

39、aca-svd矩陣分解模塊，用于按照步驟s2中過程實現將非對角塊矩陣進行壓縮分解，表示為兩個小矩陣和相乘，即，并按照步驟s3中過程完成矩陣w中所有非對角塊矩陣的壓縮分解。

40、矩陣處理存儲模塊，用于按照步驟s4中過程實現將壓縮分解后得到的疊層分塊矩陣的對角矩陣塊依次提取出來，并進行相應矩陣處理，最終將疊層分塊矩陣表示為多個塊對角矩陣相乘，然后存儲各塊對角矩陣。

41、模型訓練模塊，用于進行人工智能模型的訓練，若在此過程中用到矩陣的求逆操作，則按照步驟s5和s6實現矩陣求逆的低計算復雜度實現，并且此過程可以實現高度并行。

42、模型推理模塊，用于完成人工智能模型的推理，若在此過程中用到矩陣的求逆操作，則按照步驟s5和s6實現矩陣求逆的低計算復雜度實現，并且此過程可以實現高度并行。

43、本發明的有益效果是

44、本發明利用多層矩陣低秩壓縮技術對人工智能模型中的協方差矩陣、權重矩陣等大維度矩陣壓縮分解并轉化成多個塊對角矩陣相乘，進而協方差矩陣、權重矩陣的矩陣求逆過程可以轉化成多個塊對角矩陣的求逆，既減少了模型部署過程中矩陣存儲的資源占用，也降低了模型訓練推理過程中矩陣求逆運算的計算復雜度，并且各個塊對角矩陣相互獨立，運算過程中不存在遞歸關系，可以實現高度并行運算，充分地降低模型使用的算力門檻。

技術特征：

1.一種人工智能模型加速訓練推理方法，其特征在于，

2.根據權利要求1所述的方法，其特征在于，

3.根據權利要求1所述的方法，其特征在于，

4.根據權利要求1所述的方法，其特征在于，

5.根據權利要求1所述的方法，其特征在于，

6.根據權利要求1所述的方法，其特征在于，

7.根據權利要求1所述的方法，其特征在于，

8.根據權利要求1所述的方法，其特征在于，

9.一種人工智能模型加速訓練推理裝置，用于實現前述權利要求1所述的方法，其特征在于，

技術總結
本發明提供一種人工智能模型加速訓練推理方法及裝置，屬于人工智能領域，本發明首先利用疊層分組技術將人工智能模型中大維度矩陣進行分組拆解，轉化為疊層分塊矩陣結構；然后利用ACA?SVD矩陣分解技術將非對角塊矩陣進行壓縮分解，表示為兩個小矩陣相乘；然后將得到的疊層分塊矩陣結構的對角矩陣塊依次提取出來，將矩陣表示為多個塊對角矩陣相乘，分別存儲各個塊對角矩陣；當進行模型訓練和推理時，矩陣相乘過程可以轉化成多個塊對角矩陣相乘，矩陣求逆過程可以轉化成多個塊對角矩陣的求逆，各個塊對角矩陣相互獨立，運算過程中不存在遞歸關系，可以實現高度并行運算。

技術研發人員：張堯臣,王珂琛,李照川,林杰,王金超,郭鳳,白傳洋,王克仁
受保護的技術使用者：浪潮軟件科技有限公司
技術研發日：
技術公布日：2025/4/24