本發明屬于水下目標跟蹤領域，具體為一種模糊自適應多交互模型的多uuv協同系統水下目標跟蹤算法。

背景技術：

無人水下航行器(unmannedunderwatervehicle，uuv)水下被動目標跟蹤主要利用uuv攜帶的水聲設備被動接受水下運動目標(潛艇)的方位信息來估計目標的距離、速度和加速度等運動特性，實現對水下目標的定位與跟蹤，這種方式也被稱為純方位目標跟蹤(bearing-onlytracking)。由于該觀測方式屬于被動接受目標輻射信號，具有較強的隱蔽性，往往能給水下目標出其不意的毀滅性打擊。但是單站uuv由于獲取水下信息受限，造成觀測系統的客觀性很低，不能夠很好的獲取水下運動目標的運動信息，而多uuv協同系統組成的純方位目標跟蹤成為研究重點。

在多uuv協同系統的純方位目標跟蹤過程中,常用跟蹤算法多交互模型(interactingmultiplemodel,imm)被認為是解決水下機動目標跟蹤較好的方法之一。imm作為一種具有馬爾可夫切換系數的算法是建立在廣義偽貝葉斯算法的基礎上，其核心思想是設計模型集合來匹配和映射目標的不同運動狀態，與對應模型的濾波器并行工作,模型間利用馬爾可夫鏈以概率矩陣實現切換,各模型濾波器通過估計狀態的組合實現交互，狀態估計輸出為各個濾波器的狀態基于bayes推理的融合結果。

imm兼顧目標運動模型和濾波算法兩個方面，利用馬爾可夫過程描述模型間的轉換，對所有濾波器的輸入輸出進行加權綜合，能較好的解決單個機動目標跟蹤問題。一般地，為了更好的覆蓋水下目標運動的實際狀態，選取的運動模型越多越好，但是隨著模型數量的增加計算量會呈指數增長，同時還會引起多模型之間的無序競爭，反而降低了跟蹤算法的跟蹤精度和實時性。換句話說，imm在uuv實際應用過程中還存在以下兩個問題：(1)如何選擇和優化合適的目標運動模型，(2)如何設計合適、準確的模型轉換概率。

技術實現要素：

本發明針對多uuv協同系統的純方位目標跟蹤問題，在多交互模型imm的基礎上，提出一種模糊自適應多交互模型(fuzzyadaptiveinteractingmultiplemodel,faimm)目標跟蹤算法，主要設計目標運動模型集合(motionmodeset,mms)優化選擇和與模型轉移概率modetransitionprobability,mtp)的模糊推理，實現多uuv協同系統對水下目標的定位與跟蹤。

本發明技術方案為：

所述一種模糊自適應多交互模型的多uuv協同系統水下目標跟蹤算法，其特征在于：包括以下步驟：

步驟1：進行參數初始化，初始化參數包括模型初始概率pij(0)，最大模型概率pmax，模糊推理參數cdm和σ，采樣周期t，并確定目標運動模型集合中采用一個勻速模型和兩個協同轉彎模型；

步驟2：對于第k時刻的遞推循環估計，采用以下步驟進行：

步驟2.1：輸入交互：

根據公式

計算狀態混合估計以及協方差混合估計其中r為目標運動模型集合中的模型個數，和pⁱ(k-1|k-1)分別表示k-1時刻第i個模型的狀態估計與狀態協方差，i,j＝1,2…r，μij(k-1)為k-1時刻混合概率：

為第j個模型歸一化常數，pij(k-1)表示k-1時刻模型mi轉移到mj的轉移概率，μi(k-1)表示k-1時刻模型mi的概率；

步驟2.2：條件濾波：

以步驟2.1得到的和作為k-1時刻第j個模型的輸入，利用第j個模型對應的擴展卡爾曼濾波器進行條件濾波，計算濾波輸出和p^j(k|k)；

步驟2.3：概率更新：

根據公式

計算k時刻模型j的似然函數λj(k)，其中vj(k)為模型j的濾波新息，sj(k)為vj(k)對應的協方差；得到模型j更新后的概率為

式中

步驟2.4：根據公式

自適應推理模型轉移概率pij(k)，式中為隸屬度函數：

和分別表示隸屬度函數的中心和寬度，n表示模糊規則個數；表示第n個模糊規則對應的mtp矩陣

步驟2.5：綜合輸出：

根據公式

計算k時刻的總體估計和總體估計誤差協方差p(k|k)；

步驟3：取k＝k+1，返回步驟2，直至跟蹤結束。

有益效果

本發明在多uuv協同系統的純方位目標跟蹤過程中，選擇最少數量的目標運動集合，并通過模糊推理實現模型轉移概率的自適應變化，減少模型之間的無序競爭，濾波精確更高，能夠滿足多uuv協同系統水下目標跟蹤的需求。

本發明的附加方面和優點將在下面的描述中部分給出，部分將從下面的描述中變得明顯，或通過本發明的實踐了解到。

附圖說明

本發明的上述和/或附加的方面和優點從結合下面附圖對實施例的描述中將變得明顯和容易理解，其中：

圖1：模糊自適應多交互模型的多uuv協同系統水下目標跟蹤原理；

圖2：uuv與目標之間的相對位置關系；

圖3：高斯分布的隸屬度函數；

圖4：faimm框架設計；

圖5：faimm水下目標跟蹤軌跡；

圖6：imm水下目標跟蹤軌跡。

具體實施方式

下面詳細描述本發明的實施例，所述實施例是示例性的，旨在用于解釋本發明，而不能理解為對本發明的限制。

本實施例中，首先根據多uuv協同系統的純方位目標跟蹤原理，建立目標跟蹤系統的離散型非線性的狀態與觀測方程。其次，根據水下目標運動的特點，結合勻速模型(cv)，勻加速模型(ca),協同轉彎模型(ct),辛格模型(sg)和“當前”統計模型(cs)等常用的五種目標運動模型，依據其動力學狀態轉移矩陣進行分析，提出五種模型之間的耦合不等式關系，優化選擇適應水下目標跟蹤的運動模型集合(motionmodeset,mms)。再次，采用中間型的高斯分布函數作為隸屬度函數，將模型概率作為評價每個模型獲取濾波新息和對應的協方差的評價指標，設計模型轉移概率modetransitionprobability,mtp)的模糊推理。最后，設計與實現faimm的算法步驟，并進行實驗驗證分析。模糊自適應多交互模型的多uuv協同系統純方位水下目標跟蹤原理如圖1所示。

1.目標跟蹤原理的非線性建模

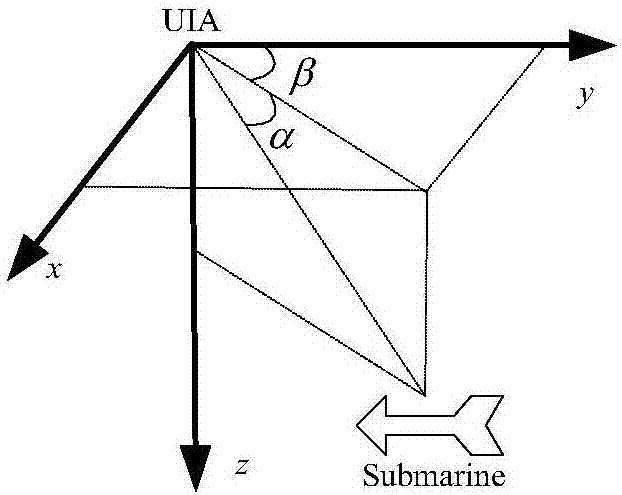
uuv觀測站點利用聲吶傳感系統對目標進行方位觀測:方位角(azimuthangle,β)和俯仰角(pitchangle,α)，其中β表征目標水平方向的位置信息，α表征目標垂直方向的位置信息。具體uuv與目標之間的相對位置關系在笛卡爾坐標系中如圖2所示。

由于水下目標跟蹤系統中背景噪聲干擾往往較大，并且目標可能會進行機動操作致使系統具有很大的隨機性和非線性。因此，目標跟蹤系統采用離散型非線性的狀態與觀測方程：

其中表示k時刻目標狀態：位置xk,yk,zk和速度信息，φ(k)表示狀態轉移矩陣，g(k)表示系統輸入噪聲矩陣，w(k)表示過程噪聲；z(k)表示觀測狀態，h(k)表示觀測矩陣,v(k)表示觀測噪聲。

在圖2中，z(k)表示觀測狀態主要包括β(k)和α(k)，其定義如：

考慮到水下目標運動具有速度慢,設定目標運動深度不變，目標深度zk為常量，則βk和αk轉化為：

其中，βk和αk的測量誤差是相互獨立的零均值高斯白噪聲v(k)＝[νβ(k),να(k)]，其方差矩陣表示為r＝diag[λβ,λα]。

2.多交互模型(imm)

多交互模型(imm)是設計模型集合來匹配和映射目標的不同運動狀態，與對應模型的濾波器并行工作,模型間利用馬爾可夫鏈以概率矩陣實現切換,各模型濾波器通過估計狀態的組合實現交互,狀態估計輸出為各個濾波器的融合結果。imm是一個遞推循環的模型，每一個遞推過程主要涵蓋四個步驟，具體分析如下：

step1輸入交互：有限模型集合m＝{m1,m2…mr},r表示模型個數,pij表示模型mi轉移到mj的轉移概率,μi(k-1)表示k-1時刻模型mi的概率,i,j＝1,2…r,則k-1時刻混合概率μij(k-1)為：

cj為第j個模型歸一化常數。

和pⁱ(k-1|k-1)分別表示k-1時刻第i個模型對應濾波器i的狀態估計與狀態協方差，i,j＝1,2…r，則狀態與協方差的混合估計分別為：

step2條件濾波：和作為k-1時刻第j個模型的輸入，利用對應的擴展卡爾曼濾波器ekf進行條件濾波，計算濾波輸出和

step3概率更新：若模型j的濾波新息vj(k)和對應的協方差sj(k)，則在k時刻模型j的似然函數λj(k)為：

則模型概率更新計算為：

式中，

step4綜合輸出(combination)：經過以上計算，則k時刻的總體估計和總體估計誤差協方差p(k|k)分別為：

3.運動模型集合mms的優化選取

imm模型應用于水下目標跟蹤時，常用的目標運動模型有以下五種：勻速模型(cv)，勻加速模型(ca),協同轉彎模型(ct),辛格模型(sg)和“當前”統計模型(cs)。根據從運動學模型角度對這五種模型進行分析，給出mms的詳細優化選取過程。

cv模型用于跟蹤勻速運動目標，其一維和二維狀態轉移矩陣分別為：

ca模型用于跟蹤勻加速直線運動目標，其一維態轉移矩陣分別為：

sg模型將目標加速度描述成時間相關隨機過程，其一維態轉移矩陣分別為：

式中，t為時間常數，1/α是一個與機動時間有關的常量，若α→∞，根據公式(14)和(15),則若α→0，根據公式(12)和(15),則可見sg模型隨著加速因子α的變化在cv和ca模型之間變化，即cv和ca模型為sg的極限形式。

cs模型采用非零均值的修正瑞利分布來表征目標機動的加速度特征，其一維態轉移矩陣與sg模型相同：

ct模型表示目標機動轉彎過程，其二維態轉移矩陣分別為：

式中，t為時間常數，w為轉角角速度，若w→0，根據公式(13)和(17),則即ct退化為cv模型，可見ct模型與cv模型具有高度的耦合性。

由公式(12)～(17)綜合可知，以上五個模型之間具有相似性和耦合性，根據運動學模型建立不等式關系：

cv＜sg＝cs≤ca＜ct(18)

根據公式(18)蘊含意義可知，sg,cs和ca模型可以根據cv與ct模型的權重之和協調獲得；同時，ct模型中雖然轉彎方向不知，但是轉彎角速度w決定的最大值一般情況下可知。因此，mms優化選取一個cv模型和兩個ct模型共三個模型可以滿足水下目標的跟蹤的需要，這樣不僅可以減少mms模型數量和計算資源，還可以確保跟蹤效果。

4.模糊推理的時變模型轉移概率設計

馬爾可夫鏈模型轉移概率mtp作為imm模型水下目標跟蹤的另一關鍵因素，其直接影響模型誤差以及模型概率估計的準確性，因此合理地選擇狀態轉移矩陣顯得尤為重要。一般情況下，imm模型之間的轉移概率在跟蹤目標時根據一定的規律性對其進行固定設置。但是，這種固定方式設置的mtp存在無用模型對有用模型的競爭，進而降低了跟蹤精確度。為此，利用模糊推理設計時變模型轉移概率(tvmtp)自適應調整模型概率，在mms確定的情況下減少無用模型對目標跟蹤精度的影響。由于模型概率μi(k)表示作為評價每個模型獲取濾波新息vi(k-1)和對應的協方差si(k-1)的評價指標。因此，tvmtp主要思想是將μi(k-1)作為模糊推理的輸入，通過模糊規則推理自動調整mtp。

由于潛艇目標在水下目標跟蹤的過程中，往往以低速進行連續機動，因此采用中間型的高斯分布函數作為隸屬度函數，具體定義為：

式中，和分別表示第i隸屬度函數的中心和寬度，n＝0,1,2…,r表示模糊規則個數，ai表示輸入變量的模糊術語，主要分為負大(recessivebig,rb),負中(recessivemedium,rm),零(zero,zo),正中(dominantmedium,dm)和正大(dominantbig,db),其分布如圖5所示。

由于模型概率μi(k-1)歸一化后其和為1，因此可以直接采用模型概率作為輸入，則rb和db中心隸屬函數設定為和zo中心隸屬函數設定rm和dm中心隸屬函數則主要根據公式(19)進行設定：如果模型之間相似度高，則接近如果模型之間相似度低，則遠離因此rm中心隸屬函數則設定為crm＝(1-cdm)/(r-1)，同時為了計算方便rb,rm,zo,dm,db的寬度設置相同

模糊規則推理計算形式建立如下：

式中，rⁿ表示第n個模糊規則，表示第n個模糊規則對應的mtp矩陣，其計算：

式中，pmax模型概率最大值。

則對應的模糊規則的解模糊計算：

式中，

pij(k)表示所求解的時變mtp,用其代替公式(4)～(5)中的模型轉移概率進行imm遞推。

根據以上分析，則形成faimm流程如圖4所示，具體步驟如下所示：

step1初始化：運動模型集合mms(1個ct模型和2個ct模型),模型初始概率pij(0)，最大模型概率pmax，模糊推理參數cdm和σ，采樣周期t；

step2利用公式(6)-(7)進行輸入交互，和

step3利用擴展卡爾曼濾波器ekf進行條件濾波，輸出和p^j(k|k)；

step4利用(8)～(9)進行模型轉移更新μj(k)；

step5利用(19)～(23)模型轉移概率mtp的自適應推理pij(k)；

step6利用(10)～(11)狀態估計輸出和p(k|k)；

step7k＝k+1，轉向step2，直到結束。

應用上述方法，本實施例中假設9個的uuv隨機靜態分布在4000×7000水下空間，對敵方潛艇目標進行跟蹤。設定uuv與潛艇固定航深，則水下三維空間退化為二維空間目標跟蹤，潛艇狀態向量為xk與yk分別表示x與y軸位置，與分別表示x與y軸速度,航深zk＝-10，起始位置x(0|0)＝[400055002525]^t，初始航向，測量噪聲方差r＝diag{σβ,σα}＝diag{0.2,0.2}。其中目標在時間1-100s,120-130s和140-200s以25m/s速度勻速直線，在時間100-120s和130-140內分別以1.62°/s和-1.62°/s進行轉彎運動。

運動模型集合mms由一個cv模型和2個ct模型組成r＝3，對應3個kf濾波器，uuv采樣周期為t＝2s，模型初始概率pij(0)＝0.33，模型概率最大值pmax＝0.98；模糊推理參數cdm＝0.66，σ＝0.33。

在上述設定條件下目標跟蹤的軌跡如圖5～6所示，同時為了驗證faimm方法的有效性，通過與imm方法在相同設定條件下使用matlab進行100次蒙特卡洛，進行統計實現根均方誤差(rmse)定量化分析如表1所示。

表1蒙特卡洛統計分析結果

從圖5和圖6對比可以看出，在開始勻速階段，faimm與imm兩種方法可以實現對目標的有效跟蹤，但是在機動轉彎過程中faimm能夠跟蹤機動過程，而imm方法則會產生較大響應延遲，隨著時間增長，產生更大誤差，同時在x-y方向位置與速度誤差都低于imm。之所以faimm能夠實現對目標運動過程的有效跟蹤得益于在保證有效且最少的運動目標集mms，并且能夠自適應調節模型概率實現了在目標運動過程的匹配，減少了目標模型之間的競爭。

總的來說，在多uuv協同系統的純方位目標跟蹤過程中，faimm優化選擇最少數量的目標運動集合，并通過模糊推理實現模型轉移概率的自適應變化，減少模型之間的無序競爭，濾波精確更高，能夠滿足多uuv協同系統水下目標跟蹤的需求。

盡管上面已經示出和描述了本發明的實施例，可以理解的是，上述實施例是示例性的，不能理解為對本發明的限制，本領域的普通技術人員在不脫離本發明的原理和宗旨的情況下在本發明的范圍內可以對上述實施例進行變化、修改、替換和變型。