本發明涉及自動化控制領域，具體涉及基于強化學習全狀態約束控制機械臂軌跡方法及系統。

背景技術：

1、智能制造和自動化成為全球制造業發展的主要趨勢。傳統的機械臂控制系統在應對復雜任務時表現出局限性，尤其在應對快速變化的生產環境時，無法靈活調整。基于強化學習的控制方法能夠讓機械臂自主學習并適應不同的生產需求，大幅提高生產效率和靈活性，減少對人工干預的依賴。

2、現代制造、服務和醫療等領域對機械臂提出了越來越復雜的操作要求。例如，在生產線、倉儲、醫療手術等環境中，機械臂必須能夠在復雜的、多變的環境中操作，同時確保精度和安全性。傳統控制方法由于對環境變化的應對能力有限，在這些應用中常常表現出不穩定。強化學習技術能夠通過與環境的持續交互學習，不斷優化軌跡控制，實現更高的靈活性和適應性。

3、機械臂的運動過程中涉及多個物理狀態，需要對這些狀態進行約束，確保任務完成的安全性和軌跡規劃的可行性。全狀態約束控制能夠實時監控并調節這些參數，避免機械臂超出其物理限制，減少故障風險，提高操作精度，特別是在涉及危險、精密操作的場景中。

4、在實際應用中，機械臂的物理模型可能不夠準確，或者環境信息可能不完全，這會給傳統基于模型的控制方法帶來困難。強化學習不依賴于精確的環境或系統模型，而是通過大量交互數據學習最佳策略，這使得它能夠在不完全信息或不確定性環境下表現出優異的性能。

5、基于強化學習的全狀態約束控制機械臂系統在工業、醫療、服務機器人、航空航天等多個領域具有廣泛應用前景。例如，在醫療領域，機械臂可以自主進行復雜的手術操作；在航空航天中，機械臂可以處理太空站中的精細任務，或在惡劣環境中修復設備。這種系統可以通過強化學習不斷提升機械臂的任務執行能力，實現更為廣泛的應用場景覆蓋。

6、機械臂軌跡跟蹤控制主要存在三個難點：

7、(1)機械臂的在不確定性和環境動態變化的場景下實現機械臂軌跡跟蹤。

8、(2)機械臂的運動中涉及許多物理和操作約束，如何在多約束條件下實現機械臂軌跡跟蹤。

9、(3)如何提高機械臂軌跡跟蹤精度。

10、在現有的基于模型預測的機械臂軌跡跟蹤控制方案中，例如現有公開文獻《基于模型預測控制的機械臂軌跡跟蹤算法》中，基于機械臂的動力學模型構建預測模型，利用當前時刻t的狀態信息q(t),預測未來n個時間步的系統狀態q(t+k)和輸出。優化目標是最小化未來時刻的軌跡跟蹤誤差和控制輸入的代價函數，常見的目標函數形式為：

11、

12、第一項表示軌跡跟蹤誤差，即預測的關節角度q(t+k)與參考關節角度qref(t+k)之間的差異。矩陣q決定了誤差的權重。第二項是控制輸入的代價，用于限制關節力矩τ(t+k)的大小，以避免過大的控制動作。矩陣r是控制輸入的權重。前述現有技術存在下述缺點：

13、(1)標準的模型預測控制方法通常假設系統是線性的或者通過線性化可以處理。如果機械臂具有顯著的非線性特性，如關節的非線性摩擦、慣性變化等，傳統的線性模型預測控制方法無法有效處理這些問題。

14、(2)模型預測控制依賴于對未來系統狀態的預測，而隨著預測時間的增加，系統模型的不確定性和環境擾動的影響會增大，導致預測結果的不準確性。即使在短期預測中，模型誤差或外部擾動也可能導致控制偏差，而長時間的預測使問題變得更復雜。

15、在現有的基于滑模控制的機械臂軌跡跟蹤方案，例如現有公開文獻《基于模糊滑模切換增益的六自由度機械臂軌跡跟蹤控制》中，滑模控制的核心是設計一個合適的滑模面，系統的狀態在滑模面上運動并最終收斂到期望值。滑模面通常定義為狀態變量的線性組合，使得系統在滑模面上運動時滿足期望的性能。常見的滑模面設計為：

16、

17、其中q是系統當前的狀態，是系統的速度，qref和是期望的軌跡和速度，λ是一個正數，控制系統的響應速度。

18、前述現有技術的存在以下缺點：

19、(1)滑模控制最顯著的缺點之一是抖振現象。當系統狀態接近滑模面時，控制輸入頻繁切換，導致系統產生高頻振蕩。這種現象稱為抖振，尤其在實際應用中，由于切換速率的有限性和傳感器的噪聲，抖振可能會影響系統的穩定性和控制精度。

20、(2)滑模控制中的切換控制律是非連續的，導致控制輸入在接近滑模面時發生頻繁變化。這種不連續性不僅是導致抖振的原因，還會在實際的執行器中帶來問題，特別是在精密控制場景下，頻繁的控制變化可能無法通過實際的硬件執行。

21、綜上，現有技術在不確定性和環境動態變化的場景下、多約束條件下，存在難以實現機械臂軌跡跟蹤、機械臂軌跡跟蹤精度較低的技術問題。

技術實現思路

1、本發明所要解決的技術問題在于：如何解決現有技術在不確定性和環境動態變化的場景下、多約束條件下，存在難以實現機械臂軌跡跟蹤、機械臂軌跡跟蹤精度較低的技術問題。

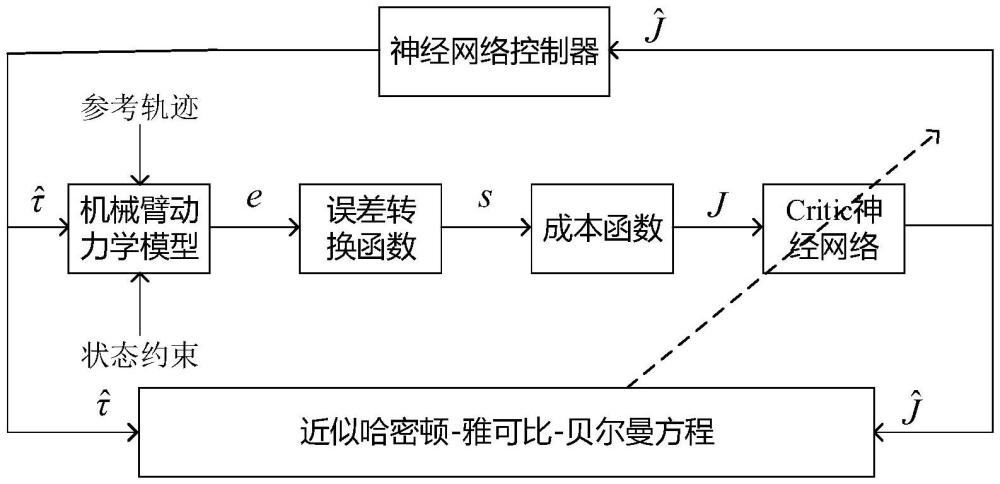
2、本發明是采用以下技術方案解決上述技術問題的：基于強化學習全狀態約束控制機械臂軌跡方法包括：

3、s1、建立n自由度旋轉關節的剛性機械臂動力學模型；

4、s2、根據剛性機械臂動力學模型，根據實際控制環境要求信息獲取狀態約束，結合狀態約束，設計誤差轉換函數，將有約束誤差e轉換為無約束誤差ξ；

5、s3、根據誤差轉換函數，處理得到并根據無約束誤差ξ的更新率，設計機械臂系統的成本函數；

6、s4、通過根據成本函數，構建雅可比-貝爾曼-哈密頓方程，并對其求解得到最優控制器、最優成本函數；

7、s5、利用critic神經網絡近似逼近最優成本函數，得到近似最優控制器；

8、s6、根據近似最優控制器，推導得近似哈密頓-雅可比-貝爾曼方程，將近似哈密頓-雅可比-貝爾曼方程和哈密頓-雅可比-貝爾曼方程做差，利用梯度下降法處理得到critic網絡的權值矩陣更新率。

9、本發明使用強化學習的方法，使用深度神經網絡作為策略網絡或價值函數網絡。本發明采用的神經網絡作為逼近復雜非線性映射的工具，因此通過深度強化學習，系統可以學習到從狀態空間到動作空間的復雜非線性關系，優化控制輸出，實現對非線性系統的良好控制。

10、本發明能夠有效地處理全狀態約束。確保在控制策略優化過程中，系統的每一個狀態變量都符合預定的約束條件，以避免系統失穩或出現違約行為。

11、本發明采用的強化學習控制方法具有較強的魯棒性，能夠在外部干擾和內部參數不確定性存在的情況下，維持軌跡跟蹤精度和系統穩定性。

12、在更具體的技術方案中，s1中，利用下述邏輯，建立剛性機械臂動力學模型：

13、

14、式中，分別表示位置矢量和速度矢量，m(q)∈rn×n表示慣性矩陣，表示科里奧利矩陣和離心矩陣，g(q)表示重力矢量，τ表示控制系統的輸入。

15、在更具體的技術方案中，s2包括：

16、s21、利用下述邏輯，利用定義系統誤差：

17、

18、式中，qd表示期望目標點是一個常數矢量；

19、s22、利用下述邏輯，定義有約束誤差e：

20、

21、s23、利用下述公式，對有約束誤差e求導數：

22、

23、s24、給定系統狀態約束，根據系統誤差，處理得到誤差約束；

24、s25、利用下述邏輯，定義誤差轉換函數，以實現系統狀態約束：

25、

26、利用下述公式，定義誤差更新率：

27、

28、其中，

29、s26、結合述有約束誤差e的導數以及誤差更新率，推得下述推導公式：

30、

31、其中，α(s)＝γa(e)，β(s)＝γb(e)。

32、在更具體的技術方案中，s24中，利用下述邏輯，給定系統狀態約束：

33、ximin<xi<ximax

34、式中，ximin和ximax分別表示系統狀態約束的下界和上界；

35、根據式(2)，處理得到誤差約束：

36、eimin<ei<eimax

37、式中，eimin和eimax分別表示誤差約束的下界和上界。

38、在更具體的技術方案中，s3中，利用下述邏輯，定義誤差轉換函數的成本函數：

39、

40、式中，q(s,τ)＝stas+τtbτ表示當地成本函數，a∈r2n×2n，b∈rn×n表示正定對稱矩陣；根據式(7)推得原始誤差代價函數v：

41、

42、以轉換后的成本函數j，作為原始誤差代價函數v的上界。

43、在更具體的技術方案中，s4包括：

44、s41、利用下述邏輯，構建可比-貝爾曼-哈密頓方程：

45、

46、s42、根據最優控制理論，根據可比-貝爾曼-哈密頓方程，處理得到下述公式：

47、

48、其中，表示最優成本函數；

49、s43、利用下述邏輯，定義最優成本函數j*：

50、

51、s44、利用下述邏輯，求解最優成本函數，得到最優控制器：

52、

53、在本發明的學習過程中，強化學習算法會根據能耗和控制精度等多重目標進行平衡，通過不斷優化控制策略，減少不必要的高頻開關操作，從而降低系統的整體能耗。此外，強化學習可以通過獎懲機制，促使系統學習到更節能的控制方法。

54、在更具體的技術方案中，s5包括：

55、s51、利用下述邏輯，利用critic網絡近似逼近最優成本函數：

56、

57、式中，wc∈rm表示權值矩陣，m表示critic網絡的隱藏節點個數，表示激活函數，ε(s)表示重構誤差；

58、s52、結合最優控制器以及式(13)，處理得到最優控制器：

59、

60、s53、將式(13)帶入可比-貝爾曼-哈密頓方程，處理得到最優可比-貝爾曼-哈密頓方程：

61、

62、其中，z＝β(s)b-1βt(s)，

63、s54、使用critic網絡近似最優成本函數，處理得到價值函數：

64、

65、其中，表示critic網絡的估計權值矩陣；

66、s55、根據價值函數，處理得到近似最優控制器：

67、

68、本發明采用的強化學習具備在線學習的能力，能夠隨著環境和系統的變化不斷調整控制策略。即使面對長時預測中的不確定性，系統也可以通過持續的學習和調整，使得控制策略能夠動態適應外部環境的變化和機械臂內部狀態的變化，從而提高軌跡跟蹤的精度和穩定性。

69、在更具體的技術方案中，s6包括：

70、s61、根據下述邏輯，利用critic網絡，處理得到近似哈密頓-雅可比-貝爾曼方程：

71、

72、s62、利用下述邏輯，定義哈密頓-雅可比-貝爾曼方程的近似誤差方程：

73、

74、s63、利用下述邏輯，定義哈密頓-雅可比-貝爾曼方程的誤差函數：

75、

76、s64、利用下述邏輯，對哈密頓-雅可比-貝爾曼方程的誤差函數進行最小化，求解得到的近似權值矩陣更新率

77、s65引入輔助項處理得到critic網絡的權值矩陣更新率。

78、本發明的強化學習通過自適應地學習控制策略，可以避免高頻的切換行為。通過策略優化，強化學習能夠生成連續和平滑的控制輸入，從而減輕甚至完全消除抖振現象。并且可以根據反饋實時調整控制策略，使得控制器在保持魯棒性的同時，避免產生高頻振蕩。強化學習可以通過優化策略來實現能耗的最小化。

79、在更具體的技術方案中，s65中，利用下述邏輯，處理得到critic網絡的權值矩陣更新率：

80、

81、式中，η1、η2表示設計正常數，v(s)表示李雅普諾夫函數，

82、在更具體的技術方案中，基于強化學習全狀態約束控制機械臂軌跡系統包括：

83、動力學模型構建模塊，用以建立n自由度旋轉關節的剛性機械臂動力學模型；

84、誤差轉換模塊，用以根據剛性機械臂動力學模型，根據實際控制環境要求信息獲取狀態約束，結合狀態約束，設計誤差轉換函數，將有約束誤差e轉換為無約束誤差ξ，誤差轉換模塊與動力學模型構建模塊連接；

85、成本函數設計模塊，用以根據誤差轉換函數，處理得到并根據無約束誤差ξ的更新率，設計機械臂系統的成本函數，成本函數設計模塊與誤差轉換模塊連接；

86、最優控制器獲取模塊，用以根據成本函數，構建雅可比-貝爾曼-哈密頓方程，并對其求解得到最優控制器、最優成本函數，最優控制器獲取模塊與成本函數設計模塊連接；

87、近似最優控制器獲取模塊，利用critic神經網絡近似逼近最優成本函數，得到近似最優控制器，近似最優控制器獲取模塊與最優控制器獲取模塊連接；

88、權值矩陣更新率獲取模塊，用以根據近似最優控制器，推導得近似哈密頓-雅可比-貝爾曼方程，將近似哈密頓-雅可比-貝爾曼方程和哈密頓-雅可比-貝爾曼方程做差，利用梯度下降法處理得到critic網絡的權值矩陣更新率，權值矩陣更新率獲取模塊與近似最優控制器獲取模塊及最優控制器獲取模塊連接。

89、本發明相比現有技術具有以下優點：

90、本發明使用強化學習的方法，使用深度神經網絡作為策略網絡或價值函數網絡。本發明采用的神經網絡作為逼近復雜非線性映射的工具，因此通過深度強化學習，系統可以學習到從狀態空間到動作空間的復雜非線性關系，優化控制輸出，實現對非線性系統的良好控制。

91、本發明能夠有效地處理全狀態約束。確保在控制策略優化過程中，系統的每一個狀態變量都符合預定的約束條件，以避免系統失穩或出現違約行為。

92、本發明采用的強化學習控制方法具有較強的魯棒性，能夠在外部干擾和內部參數不確定性存在的情況下，維持軌跡跟蹤精度和系統穩定性。

93、在本發明的學習過程中，強化學習算法會根據能耗和控制精度等多重目標進行平衡，通過不斷優化控制策略，減少不必要的高頻開關操作，從而降低系統的整體能耗。此外，強化學習可以通過獎懲機制，促使系統學習到更節能的控制方法。

94、本發明采用的強化學習具備在線學習的能力，能夠隨著環境和系統的變化不斷調整控制策略。即使面對長時預測中的不確定性，系統也可以通過持續的學習和調整，使得控制策略能夠動態適應外部環境的變化和機械臂內部狀態的變化，從而提高軌跡跟蹤的精度和穩定性。

95、本發明的強化學習通過自適應地學習控制策略，可以避免高頻的切換行為。通過策略優化，強化學習能夠生成連續和平滑的控制輸入，從而減輕甚至完全消除抖振現象。并且可以根據反饋實時調整控制策略，使得控制器在保持魯棒性的同時，避免產生高頻振蕩。強化學習可以通過優化策略來實現能耗的最小化。

96、本發明解決了現有技術在不確定性和環境動態變化的場景下、多約束條件下，存在難以實現機械臂軌跡跟蹤、機械臂軌跡跟蹤精度較低的技術問題。